ответ: Mod(CB)+Mod(CD)=10+24=34 cm
Mod (CB+CD)=26 cm
Mod(BA)-Mod(DA)=10-24=-14 cm
Mod(BA-DA)=26cm
Объяснение:
1.Mod(CB)+Mod(CD)=10+24=34 cm , Так как Mod(CB)-это просто длина вектора СВ , а Mod(CD)- просто длина вектора CD
2.CB+CD=CA (сложение по правилу параллелограмма) ,
Mod (CА)= длина СА - находим по т.Пифагора.
СА= sqrt (24²+10²) =sqrt(676) =26 cm=> Mod(CB+CD)=26 cm
3. Mod(BA)-Mod(DA)=10-24=-14 cm -По той же причине, что и пункт первый задания. , так как Mod(BА)-это просто длина вектора СВ , а Mod(DА)- просто длина вектора DА
4. BA-DA=BA+AD=BD
Длину BD опять находим по т. Пифагора
BD= sqrt (24²+10²) =sqrt(676) =26 cm=> Mod(BA-DA)=26 cm .
ответ: 1 сторона=6см
2сторона=10см
3 сторона 14см
Р=30см
Объяснение: обозначим вершины треугольника А В С, пропорции 3: 5 : 7 как АВ=3х, ВС=5х, АС=7х и зная, что периметр треугольника составляет 60см составим уравнение:
3х+5х+7х=60
15х=60
х=60÷15
х=4
Теперь найжем каждую сторону треугольника:
1) АВ=3х=3×4=12см
2)ВС= 5х=5×4=20см
3) АС=7х=7×4=28см
Так как треугольник DEF вписан в ∆АВС с середин сторон, то по правилам средней линии треугольника, средняя линия параллельная одной из его сторон равна половине этой стороны.
Поэтому EF || АВ и EF=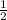
×AB =12÷2=6 см
DF || BC и EF=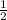
×BC=20÷2=10см
DE || AC; DE=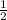
×AC=28÷2=14см
тогда периметр второго треугольника составит: Р=6+10+14=30см