
Объяснение:
всё правильно в онлайн мектеп проверяла
Объем пирамиды равен одной трети произведения ее высоты на площадь основания.
V=⅓ S∙h
Основание правильного шестиугольника состоит из шести правильных треугольников.
Площадь правильного треугольника находят по формуле:
S=(а²√3):4
S=4√3):4=√3
Площадь правильного шестиугольника в основании пирамиды:
S=6√3
Высоту найдем из прямоугольного треугольника АВО:
Так как ребро образует с с диагональю основания угол 60°, высота пирамиды ВО равна
H=ВО=2:ctg (60°)= 2·1/√3=2√3
Можно найти высоту и по т. Пифагора с тем же результатом.
V= 2√3∙6 √3:3=12 (кубических единиц)
Подробнее - на -
Объяснение:
Основание пирамиды прямоугольник.
Его площадь 12•5=60 см²
Диагонали прямоугольника равны и в точке пересечения делятся пополам ⇒АО=ОВ=ОС=OD. Эти половинки диагоналей - проекции ребер пирамиды. Следовательно, ребра пирамиды как наклонные с равными проекциями равны. SA=SD=SC=SB
Боковые грани – 2 пары равных равнобедренных треугольников с основаниями 12 см и 15 см.
Высота SМ в ∆ASB=√(SO*+OM*)=√(64+6,25)=0,5√281
Высота SН в ∆BSC=√(SO²+OH²)=√(64+36)=10 см
S ∆ASB=AM•SM=6•0,5√281=3√281 см²
S ∆ BSC=BH•SH=2,5•10=25 см²
S бок=2•3√281+2•25=(6√281+50) см² или ≈150,58 см²
S полн=60+60√281+50=(110+60√281) см² или ≈210,58 см²
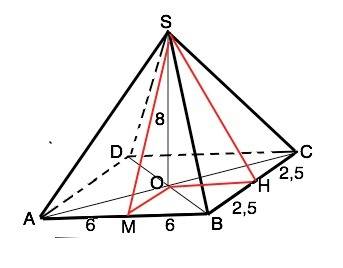
ответ: вообщем вот фото, тут все написано.