ответ:Найди площадь круга, вписанного в равнобедренную трапецию с основаниями длиной 6 см и 12 см и периметром 36 см
Объяснение:
АВСМ- описанная трапеция⇒ суммы длин противоположных сторон равны. Т.е 6+12=АВ+СМ⇒ АВ=СМ=9 см. Пусть ВК⊥АМ , СР⊥АМ.
S(круга)=πr². Радиус вписанной в трапецию окружности будет равен половине высоты трапеции.
Т.к. ВК⊥АМ , СР⊥АМ, то КВСР-прямоугольник ⇒
КР=6 см, АК=РМ=(12-6) :2=3 (см).
ΔАВК-прямоугольный, по т. Пифагора :
ВК=√(9²-3²)=√((9-3)(9+3))=√(6*12)=6√2(см).
ВК-высота трапеции, значит r=3√2 см.
S(круга)= π (3√2 )²=18π (см²).
https://seoi.net/peni3d/
Пусть одна сторона равна х, тогда смежная с ней, по условию задачи, равна х + 5 (см).
Площадь прямоугольника равна произведению двух его смежных сторон.Следовательно -
х*(х + 5) = 24
х² + 5х = 24
х² + 5х - 24 = 0
а = 1, b = 5, с = -24
D = b² - 4ac = 5² - 4*1*(-24) = 25 + 96 = 121
√D = √121 = 11.
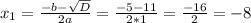
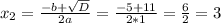
x₁ - не удовлетворяет условию задачи, так как длины сторон не могут быть выражены отрицательным числом.
Следовательно, остаётся, что х = 3.
Первая сторона = х = 3 (см)
Вторая сторона = х + 5 (см) = 3 (см) + 5 (см) = 8 (см).
Для окончательного ответа нужно учесть, что -
Противоположные стороны прямоугольника равны.3 (см), 8 (см), 3 (см), 8 (см).
треугольник со сторонами 18см,24см,30см-прямоугольный
S= 18*24/2=216 см2