Правильная четырёхугольная призма.
АВ = 4 см.
AC1 = 4√3 см.
Найти:V - ?
Решение:"Правильный многоугольник - многоугольник, у которого все углы и стороны равны".
Так как данная призма - правильная, четырёхугольная => основание этой призмы - квадрат.
"Квадрат - геометрическая фигура, у которой все стороны равны".
=> АВ = AD = CD = CB = 4 см.
АС - диагональ квадрата.
d = a√2, где d - диагональ квадрата АС; а - сторона квадрата.
=> АС = 4√2 см.
СС1 = h призмы.
Найдём СС1 (h), по теореме Пифагора: (с = √(a² + b²), где с - гипотенуза; а, b - катеты)
a = √(c² - b²) = √((4√3)² - (4√2)²) = 4 см.
Итак, СС1 = h = 4 см.
V = S основания * h
Основание - квадрат.
S квадрата = а² = 4² = 16 см.
V = 16 * 4 = 64 см³
ответ: 64 см³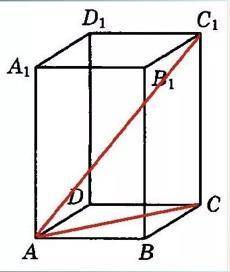
Без ответов
Теги
Пользователи
0 Свойство катета прямоугольного треугольника - Геометрия 7 класс
Открыт 1 ответов 1152 Просмотров Геометрия
Оказалось, что простатит боится, как огня именно это ...
Вы больше никогда не вспомните о простатите
ПОДРОБНЕЕ
Система заработка, которая стреляет без промаха! От $1000 в ...
От вас только требуется запустить это видео! Я разбогатела ...
ПОДРОБНЕЕ
Один из острых углов прямоугольного треугольника равен 60°, а сумма короткого катета и гипотенузы равна 33 см.
Определи длину короткого катета.
1. Величина второго острого угла равна °
2. Длина короткого катета равна
см.
спросил 16 фев, 15 от it всезнающее око (72, ) в категории геометрия
Пометитьответить
1 ответ
kola99
132, Зарегистрированный пользователь
0
1. Если один из острых углов прямоугольного треугольника равен 60°, то другой острый угол равен 30°.
2. Значит острый угол, который равен 30°, является меньшим углом прямоугольного треугольника, а напротив меньшего угла расположена меньшая сторона.
Катет напротив угла равного 30° равен половине гипотенузы.
Если обозначить короткий катет через x, то
x+2x=333x=33x=33:3x=11