Вариант-2. 1. Диагонали прямоугольника MNKP пересекаются в точке 0, L MON=64°.
Найдите угол ОМР.
2. Найдите углы равнобедренной трапеции, если один из его углов на 30° больше
другого.
3. Стороны параллелограмма относятся как 3:1, а его периметр равен 40 см.
Найдите стороны параллелограмма.
4. В прямоугольной трапеции разность углов при одной из боковых сторон равна
48°. Найдите углы трапеции.

👇

Открыть все ответы

Ответ:

хорошист488

02.09.2022

В трапецию ABCD вписана окружность, которая касается боковой стороны AB в точке K. Известно, что AK =8 , KB= 3. Найдите радиус окружности.

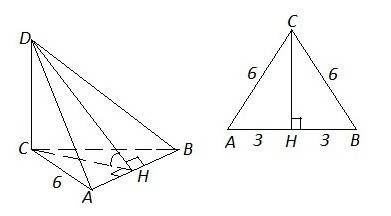
Решение возможно в двух вариантах:

1) r = √(8*3) = √24 = 2√6 ед (на основании свойства высоты из прямого угла).

2) Примем О - центр вписанной окружности,
х - отрезок ВО.
у - отрезок АО.
Составляем систему из трёх уравнений:
{9 + r² = x²;
{64 + r² = y²;
{x² + y² = (8+3)².
Подставим в третье уравнение x² + y² = 9 + r² + 64 + r² = 2r² + 73.
Получим 2r² + 73 = 121,
r² = (121 - 73)/2 = 48/2 = 24.
Тогда r = √24 = 2√6 ед.

4,7(59 оценок)

Ответ:

плюхплюх

02.09.2022

Чтобы определить линейный угол двугранного угла, надо к линии пересечения плоскостей (граней угла) провести перпендикуляры в обеих плоскостях. Угол между проведёнными перпендикулярами и будет искомым углом. Удобно, когда перпендикуляры проводятся из одной точки,лежащей на линии пересечения.Определим линейный угол двугранного угла DABС. Линия пересечения плоскостей - АВ. Точка D лежит в пл. АВD , а точка С - в пл. АВС. Проведём СH⊥AB в пл АВС ⇒ СH явл. перпендикуляром в пл. AВС к АВ. СH явл. также биссектрисой и медианой, т.к. ΔАВС равносторонний, все его стороны = 6 , ВН=6:2=3, СН=√(АС²-АН²)=√(6²-3²)=√(36-9)=√27=√(9·3)=3√3 .
Соединим точку D и Н. DH - наклонная, DС - перпендикуляр к пл. АВС ⇒СН - проекция наклонной DH на пл. АВС. Т.к. проекция СН ⊥АВ ⇒ по теореме о трёх перпендикулярах тогда и наклонная DH⊥AB. DH явл. перпендикуляром к АВ в пл. ABD.Найдём DН из ΔABD. ⇒ DH=√(DB²-BH²)=√((3·√7)²-3²)=√(9·7-9)=√54=√(9·6)=3√6 .
Получили, что DH⊥AB и CH⊥AB ⇒ линейный ∠DHC - есть линейный угол двугранного угла DABC. (Из сказанного следует ещё,что AB⊥пл.DCH)∠DHC найдём из ΔDCH. ∠DCH=90°, cos∠DHC=CH/DH=(3√3)/(6√3)=√(3/6)=√(1/2)=1/√2=√2/2 ⇒ ∠DHC=45°.
Двугранному углу DACB соответcтвует линейный угол DCB, т.к. пл.ВАС перпендикулярна пл.DAC , то ∠DCB=90°.
Двугранному углу BDCA соответствует линейный ∠АСВ, т.к. DС⊥AC и DC⊥BC.∠АСВ=60° как угол равностороннего треугольника .
ответ: 90° , 45° , 60° .

С: ребро cd треугольной пирамиды abcd перпендикулярно к плоскости авс. найдите друхгранные углы dacb