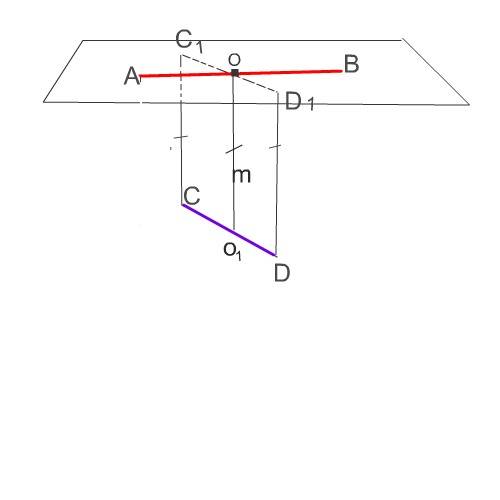
Обозначим скрещивающиеся прямые АВ и СD. Отметим на прямой АВ точку О.
1. Через прямую и не лежащую на ней точку можно провести плоскость, и притом только одну. Проведем эту плоскость через точку О и прямую СD.
2. Соединим центр СD с точкой О. От концов СD проведем отрезки, параллельные и равные первой прямой. Обозначим их концы С₁ и D₁ соединим.
Мы получили две пересекающиеся прямые АВ и С₁D₁, через которые можно провести плоскость, и притом только одну. Проведенная таким образом плоскость параллельна прямой СD.
Медиана делит исходный треугольник на 2 равнобедренных, основаниями которых являются боковые стороны. Угол А медианой делится на 2угла, один из которых равен углу В, другой - углу С. Следовательно, угол А равен сумме двух других углов.
Думаю, ответ будет понятен и без рисунка.
Если медиана треугольника равна половине стороны, к которой проведена, этот треугольник - прямоугольный. ( Обратное утверждение того, что медиана прямоугольного треугольника, проведенная из вершины прямого угла к гипотенузе, равна половине гипотенузы).