запомни таблицу состояние вещей из как расположена молекул или от ума между собой основные свойства примеры веществ схема структура вещества рисовать структуру веществ
Площадь треугольника CDE равна половине произведения стороны CD на высоту, опущенную на неё из вершины E (обозначим её ). Тогда справедливо следующее равенство:
Аналогично в треугольнике ABE:
Поскольку перескающиеся диагонали в трапеции отсекают подобные треугольники (ABE и CDE), найдём коэффициент подобия:
Поскольку в подобных треугольниках соответствующие элементы пропорциональны, то справделивы следующие соотношения:
Площадь трапеции ABCD равна произведению полусуммы её оснований (AB и CD) на высоту, которая равна сумме и , то есть
Для доказательства равенства ABD = DCA на рисунке 7, воспользуемся данной информацией:
а) Если угол 1 равен углу 2 и AC равно BD.
1. Рассмотрим треугольник ABC и треугольник CDA. У нас есть две известные информации: угол 1 равен углу 2 и AC равно BD.
2. Углы, лежащие на одном луче, которые равны друг другу, называются вертикальными углами. Таким образом, угол ABC равен углу ADC из-за данного условия.
3. Когда два угла в одном треугольнике равны двум углам в другом треугольнике, то такие треугольники называются равными по 3 углам. Значит, треугольник ABC равен треугольнику ADC.
4. По определению, равные двум прямым треугольникам равны и соответствующие стороны. Так как AC равно BD, то AB равно CD, и соответствующие стороны треугольников ABC и CDA равны.
5. Таким образом, мы доказали, что угол ABD равен углу DCA, если угол 1 равен углу 2 и AC равно BD.
б) Если угол 1 равен углу 2, BO равно OC и AB равно CD.
1. Рассмотрим треугольник ABC и треугольник CDA. У нас есть три известные информации: угол 1 равен углу 2, BO равно OC и AB равно CD.
2. Углы, лежащие на одном луче, которые равны друг другу, называются вертикальными углами. Таким образом, угол ABC равен углу ADC из-за данного условия.
3. Когда два угла в одном треугольнике равны двум углам в другом треугольнике, то такие треугольники называются равными по 3 углам. Значит, треугольник ABC равен треугольнику ADC.
4. По определению, равные двум прямым треугольникам равны и соответствующие стороны. Так как AB равно CD, то AC равно BD, так как BO равно OC. Следовательно, соответствующие стороны треугольников ABC и CDA равны.
5. Таким образом, мы доказали, что угол ABD равен углу DCA, если угол 1 равен углу 2, BO равно OC и AB равно CD.
Таким образом, независимо от условий, мы доказали, что угол ABD равен углу DCA на рисунке 7.
242
Объяснение:
Площадь треугольника CDE равна половине произведения стороны CD на высоту, опущенную на неё из вершины E (обозначим её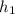
). Тогда справедливо следующее равенство:
Аналогично в треугольнике ABE:
Поскольку перескающиеся диагонали в трапеции отсекают подобные треугольники (ABE и CDE), найдём коэффициент подобия:
Поскольку в подобных треугольниках соответствующие элементы пропорциональны, то справделивы следующие соотношения:
Площадь трапеции ABCD равна произведению полусуммы её оснований (AB и CD) на высоту, которая равна сумме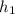
и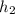 
, то есть