В пирамиде МАВС плоскости МА – высота. В треугольнике АВС АВ = АС; АК – медиана. Указать линейный угол двугранного угла при ребре ВС. А) МВА; Б) МСА; В) МАК; Г) МКА

В пирамиде МАВС плоскости МА – высота. В треугольнике АВС АВ = АС; АК – медиана. Указать линейный уг

👇

Увидеть ответ

Ответ:

alinakyberskaya

20.06.2021

Г) МКА

Объяснение:

Так как AB = AC, то ABC - р/б треугольник, тогда АК - это и его высота. Линейный угол двугранного угла измеряется углом, образованным пересечением двугранного угла с плоскостью, перпендикулярной к его ребру, то есть нам подходит угол МКА

4,8(46 оценок)

Открыть все ответы

Ответ:

notix55

20.06.2021

ответ:

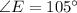
$\angle E=105^{\circ}$

Объяснение:

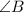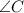Проведём биссектрисы $\angle B$ и $\angle C$ . Пусть они пересекаются в точке .

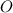Также проведём отрезки 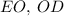$EO, \: OD$ и .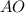

========================================

Рассмотрим 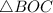$\triangle BOC$ :

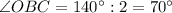$\angle OBC = 140^{\circ}:2=70^{\circ}$ , т.к. 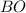- биссектриса.

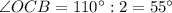$\angle OCB=110^{\circ}:2=55^{\circ}$ , т.к. 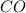- биссектриса.

Сумма внутренних углов треугольника равна 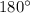$180^{\circ}$ .

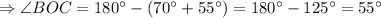
$\Rightarrow \angle BOC=180^{\circ}-(70^{\circ}+55^{\circ})=180^{\circ}-125^{\circ}=55^{\circ}$

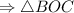$\Rightarrow \triangle BOC$ - равнобедренный.

========================================

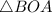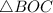Рассмотрим $\triangle BOA$ и $\triangle BOC$ :

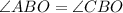$\angle ABO=\angle CBO$ , т.к. 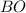- биссектриса;

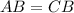AB=CB (по условию); 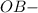OB - общая сторона.

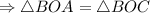$\Rightarrow \triangle BOA=\triangle BOC$ (по I признаку равенства треугольников).

========================================

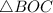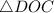Рассмотрим $\triangle BOC$ и $\triangle DOC$ :

$\angle BCO=\angle DCO$ , т.к. 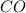- биссектриса;

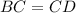BC=CD (по условию), 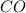- общая сторона.

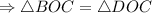$\Rightarrow \triangle BOC=\triangle DOC$ (по I признаку равенства треугольников).

========================================

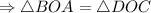$\Rightarrow \triangle BOA=\triangle DOC$ , т.е. мы имеем три равных равнобедренных тр-ка:

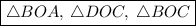
$\boxed{\triangle BOA, \: \triangle DOC,\: \triangle BOC}$

========================================

Рассмотрим 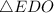$\triangle EDO$ :

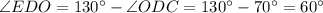$\angle EDO=130^{\circ}-\angle ODC=130^{\circ}-70^{\circ}=60^{\circ}$ .

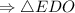$\Rightarrow \triangle EDO$ - равносторонний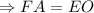 $\Rightarrow FA=EO$

========================================

Рассмотрим геометрическую фигуру 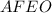AFEO :

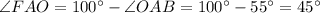$\angle FAO=100^{\circ}-\angle OAB=100^{\circ}-55^{\circ}=45^{\circ}$ .

$\angle AOE=360^{\circ}-(55^{\circ}+55^{\circ}+55^{\circ}+60^{\circ})=135^{\circ}$ (т.к. в полном угле всего 360°)

При пересечении двух параллельных прямых секущей, сумма односторонних углов равна 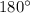$180^{\circ}$ .

$\angle FAO+\angle EOA=180^{\circ} \Rightarrow FA|| EO$

Если у геометрической фигуры есть 4 угла, 4 стороны, а 2 стороны равны и параллельны, то этот четырёхугольник - параллелограмм.

У параллелограмма противоположные углы равны.

$\Rightarrow \angle FAO=\angle FEO=45^{\circ}$ .

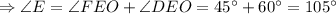
$\Rightarrow \angle E=\angle FEO+\angle DEO=45^{\circ}+60^{\circ}=105^{\circ}$

========================================

В шестиугольнике ABCDEF выполнены равенства FA=AB=BC=CD=DE, ∠A=100∘, ∠B=140∘, ∠C=110∘, ∠D=130∘. Найд

4,7(41 оценок)

Ответ:

Q778

20.06.2021

ответ: S=9см²

Объяснение: площадь трапеции с диагоналями пересекающимися под прямым углом вычисляется по формуле:

S=d²/2

Так как трапеция равнобедренная, то АВ=СД, и диагонали АС=ВД и при пересечении они делятся на одинаковые отрезки. Найдём величину диагонали. Диагонали АС и ВД образуют при пересечении 2 равнобедренных прямоугольных треугольника ВОС и АОД, в которых ВО=СО и АО=ДО , которые являются катетами, а ВС и АД - гипотенузы. Катет равнобедренного прямоугольного треугольника меньше гипотенузы в √2 раз, поэтому ВО=СО=2/√2см, а

АО=ДО=4/√2см.

Тогда АС=ВД=4/√2+2/√2=6/√2

Теперь найдём площадь трапеции зная её диагонали:

S=(6/√2)²÷2=36÷2÷2=9см²