В прямом параллелепипеде стороны равны 3 см и 8 см, угол между ними 60°. Площадь боковой поверхности параллелепипеда 220 см². Найдите меньшую диагональ параллелепипеда.
* * *
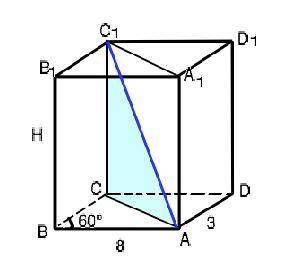
На рисунке меньшая диагональ АС1 соединяет вершины тупых углов противоположных оснований.
Для решения требуется найти высоту СС1 и диагональ АС основания. S (бок)=Р•Н, где Р - периметр основания параллелепипеда, Н - его высота. ⇒ Н=220:2•(8+3)=10 см.
По т.косинусов АС²=ВС²+АВ²-2ВС•АС•cos60° ⇒ АС²=9+64 - 2•24•1/2 ⇒ АС²=49.
Из ⊿ АСС1 по т.Пифагора АС1=√(AC²+CC1²)=√(100+49)=√149 см, т.е. ≈12,2 см
рассмотрим треугольник ahc-прямоуг., равнобедренный ah=ch=x, ac^2=ah^2+ch^2,
2^2=x^2+x^2
4=2x^2
2=x^2
x=корень из 2
рассмотрим треугольник chb, по теореме пифагора
cb^2=ch^2+hb^2
cb^2= 3^2+(корень из 2)^2=9+2=11
cb= корень из 11