1.
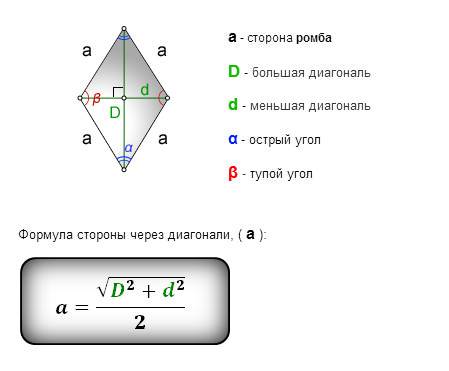
Формула в 1 вложении.
а=5, d=6
D^2 = 4a^2 - d^2
D=8
2.
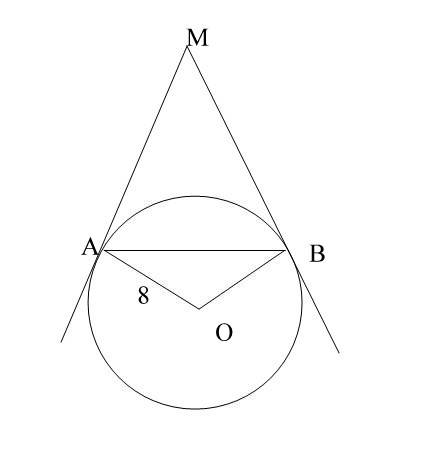
Ма и Мв-касательные, АВ-секущая.
Угол, образованный касательной к окружности и секущей, проведенной через точку касания, равен половине дуги, заключенной между его сторонами.
Т.е. угол МАВ=60 гр. и угол МВА=60 гр. Следовательно, треугольник АМВ-равносторонний.
Проведем из т.О перпендикуляр ОЕ к секущей АВ.
Рассмотрим треугольник АЕО-прямоугольный.
АО=r=8, угол ОЕА=90 гр, угол АОЕ=60 гр, следовательно, угол ОАЕ=30 гр.
Катет, лежащий напротив угла 30 градусов, равен половине гипотенузы.
ОЕ=1/2АО
ОЕ=4
AE^2 = AO^2 - OE^2
АЕ=корень из 48.
АВ=АЕ+ЕВ=2 корня из 48=8 корней из 3.
Р=3*8 корней из 3 = 24 корня из 3.
Дано угол альфа и периметр. См. рисунок. Допустим, что треугольник построен АВС, угол А - данный угол альфа. Отложим на прямой АС отрезки СЕ=ВС и АД=АВ. Угол Е очевидно 45 град. Угол ВАС - внешний для треуг. АДВ, равен сумме углов Д и ДВА, откуда угол Д равен альфа/2. Отрезок ДЕ равен периметру. ЧТо это нам дает? Угол 45 и альфа/2 легко построить, а значит легко найти точку В, из нее опускаем перпендикуляр на ДЕ и получаем точку С треуг. АВС, того что надо построить. Теперь надо найти точку А, она как видно равноудалена от точек Д и В, т.е. лежит на сред.перпендикуляре к отрезку ВД, это тоже легко построить и пересечением его с ДЕ найдем А. т.е. весь треуг. будет построен.