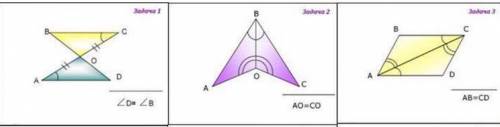
ABCD - выпуклый четырехугольник, в нем по условию ∠BAC=∠ACD, а это внутренние накрест лежащие при прямых СD и АВ, и секущей АС, значит, по признаку параллельности прямых СD и АВ параллельны. ВC=AD.
Четырехугольник окажется вписанным, если сумма противоположных углов равна 180°. Параллелограмм, который вписан в окружность, может быть только прямоугольником. /как частный случай прямоугольника - квадрат./
А если стороны АD и ВС не параллельны, то это будет равнобедренная трапеция.
Равнобедренной трапецией этот четырехугольник будет,
если добавить условия
1) AB≠CD; /верхнее и нижнее основания у трапеции различные./ и
6)BC не параллелен AD;/боковые стороны не параллельны/, 7) ∠BCA≠∠CAD; /при равенстве этих углов противолежащие углы равны, в сумме 180°, тогда трапеция не получим./
Если же добавить условие 8)∠ABC=90∘ то и угол С станет тоже прямым, поскольку ВС будет перпендикулярно к одной из двух параллельных прямых АВ, он окажется перпендикуляром и к СD, 3)AD>AB; значит, четырехугольник окажется прямоугольником. около него тоже можно описать окружность, центр ее - точка пересечения
диагоналей. если не учитывать 3)AD>AB, то можем допустить, что эти смежные стороны равны, тогда из прямоугольника получим квадрат.
наконец, окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников. Но данных в условии не хватает для этого.
ответ 1), 6), 7, или 8)
Площадь круга, как Вы помните, находят по формуле
S=πr²
Радиус находим из остроугольных треугольников, образовавшимися диагоналями при меньшей стороне прямоугольника.
Эти треугольники - равносторонние, т.к. угол при пересечении диагоналей равен 60°, а сами диагонали делятся пополам и этим образуют равнобедренные треугольники, углы которых при основании, равном меньшей стороне вписанного прямоугольника, тоже равны 60°.⇒cледовательно, каждая половина диагонали равна меньшей стороне прямоугольника. А так как диагонали здесь являются диаметрами окружности, то радиус описанного круга тоже равен меньшей стороне прямоугольника.
r=10 см
S=πr²,
S=100 π см²