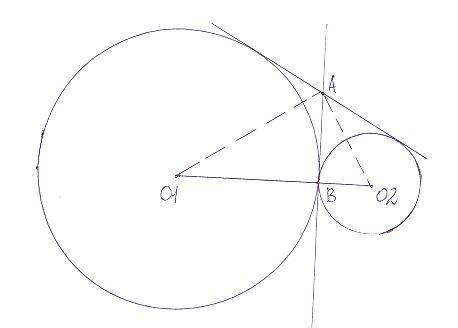
вот вам рисунок
Решение очень простое - вся "хитрость" в том, что угол О1АО2 (между пунктирными прямыми) равен 90 градусам. Дело в том, что О1А и О2А - биссеткриссы смежных углов (почему биссектрисы, - это понятно? обоснуйте), а сумма смежных углов 180 градусов. Ну, сумма половин смежных углов (то есть сумма угла О1АВ и угла О2АВ) дает 90.
Таким образом, трегольник О1АО2 - прямоугольный, и АВ - высота к гипотенузе.
Дальше - очень полезное "заклинание" - хотя и очень простое.
Высота к гипотенузе делит прямоугольный треугольник на два, подобные ему - и между собой тоже, конечно.
Поэтому
О1B/АВ = АВ/О2В;
О1B = АВ^2/O2B = 6^2/4 = 9;
Пусть ABC - равнобедренный
∟B = 120 °, АС = 18 см, АК - высота.
В ΔАВС проведем высоту BD к основанию АС.
По свойству равнобедренного треугольника BD - биссектриса и медиана
AD = DC = 1 / 2AC = 18: 2 = 9 (см) (BD - медиана).
∟AВD = ∟DBC = 1 / 2∟В = 120 °: 2 = 60 ° (BD - биссектриса).
Рассмотрим ΔABD - прямоугольный (∟D = 90 °, BD - высота):
∟BAD + ∟ABD = 90 °; ∟BAD = 30 °; ∟BAD = ∟BCD = 30 ° (ΔABC - равнобедренный).
Рассмотрим ΔАКС (∟К = 90 °, АК - высота):
АК - катет, лежащий напротив угла 30 °, тогда АК = 1 / 2АС; АК = 18: 2 = 9 (см).
ответ: Высота AK= 9 см
Большее основание равнобедренной трапеции равно а, острый угол равен а.
Трапеция вращается вокруг ее большего основания.
Отношение радиуса круга, описанного около трапеции, к радиусу круга, вписанного в нее, равно k.
В основании прямой призмы лежит равнобедренная трапеция, диагонали которой перпендикулярны соответствующим боковым сторонам.
Угол между диагоналями трапеции, противолежащий ее боковой стороне, равен а.
В основании четырехугольной пирамиды лежит равнобедренная трапеция с основаниями а и Ь (а > 2й) и углом q> между неравными отрезками ее диагоналей.
Основанием пирамиды служит равнобедренная трапеция с острым углом а.
Эта трапеция описана около окружности основания конуса.
Сооружается участок железнодорожной насыпи длиной 100 м, поперечным сечением которого является равнобедренная трапеция с нижним основанием 5 м, верхним основанием, не меньшим 2 м, и углом откоса 45°.
Площадь криволинейной трапеции аАВЬ (рис.
Определить длины сторон прямоугольника наибольшей площади, вписанного в прямоугольную трапецию с длинами оснований 24 и 8 см и длиной высоты 12 см (две вершины прямоугольника лежат на боковых сторонах трапеции, а две другие — на ее большем основании).
Боковая сторона равнобедренной трапеции равна ее меньшему основанию.
Величина угла при вершине А трапеции ABCD равна а.
Доказать, что в любой трапеции ABCD (рис.
Доказать, что прямая, проходящая через полученную точку и точку пересечения диагоналей, делит каждую из параллельных сторон трапеции на две равные части.