a) Расстояние до хорды измеряется перпендикуляром, оопущенным из центра окружности к хорде. По свойству хорд радиус, перпендикулярный к хорде, делит эту хорду пополам. CH=HD=CD/2=9см. OD-радуис = AB/2=15см. По теореме Пифагора находим
OH=12
b) По тем же соображениям находим радиус окружности (OD), если HD=CD/2=6см, а OH=8.
OD=10см
с) И наконец если радиус окружности OD=52/2=26см, а OH=10см, то HD= 24, CD=2*24=48см
1. Задача 1. решена пользователем ХироХамаки Новичок (решение в файле)
2. Условие задачи 2. неточное. Должно быть: Основание АС равнобедренного треугольника лежит в плоскости α. Найдите расстояние от точки В до плоскости α, если АВ = 5, АС = 6, а двугранный угол между плоскостью треугольника и плоскостью α равен 60 градусам.
Проведем ВН⊥АС и ВО⊥α. ВО - искомое расстояние. ОН - проекция ВН на плоскость α, значит ОН⊥АС по теореме, обратной теореме о трех перпендикулярах. ∠ВНО = 60° - линейный угол двугранного угла между плоскостью α и плоскостью треугольника. АН = НС = 6/2 = 3 (ВН - высота и медиана равнобедренного треугольника) ΔАВН: по теореме Пифагора ВН = √(АВ² - АН²) = √(25 - 9) = √16 = 4 ΔВНО: ВО = ВН · sin 60° = 4 · √3/2 = 2√3
3. АО⊥α, ОВ и ОС - проекции наклонных АВ и АС на плоскость α, тогда ∠АВО = ∠АСО = 60°. ΔАВО = ΔАСО по катету и противолежащему острому углу (АО - общий катет и ∠АВО = ∠АСО = 60°), значит АВ = АС = 6.
Рисунок вам нарисовала. Там все ясно-понятно. Треугольник FAB равносторонний. Все стороны равны, все углы по 60, такой вывод делаем из условия. Сторону этого треугольника обозначаем х. Δ FMA: М = 90 FM - бисектриса, медиана, высота FM = хsina = x√3/2 Чтобы найти угол между мимобегущими, нужно найти угол между паралельными им прямыми, которые пересекаются. Перенесем AC в ML, это будет средняя линия треугольника ABC Чтобы узнать AC найдем диагональ квадрата d² = 2a² Сторона у нас х d² = 2x² d = x√2 ML = x√2/2 ΔFMO₁ (O₁ = 90) MO₁ = x√2/4 MO₁/FM = cos a = x√2/4/x√3/2 = √2/2√3 = √6/6 Не знаю, почему значение не табличное, может я ошиблась, но вроде все правильно было :)
а) 12см b) 10см c) 48см
Объяснение:
a) Расстояние до хорды измеряется перпендикуляром, оопущенным из центра окружности к хорде. По свойству хорд радиус, перпендикулярный к хорде, делит эту хорду пополам. CH=HD=CD/2=9см. OD-радуис = AB/2=15см. По теореме Пифагора находим
OH=12
b) По тем же соображениям находим радиус окружности (OD), если HD=CD/2=6см, а OH=8.
OD=10см
с) И наконец если радиус окружности OD=52/2=26см, а OH=10см, то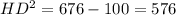
HD= 24, CD=2*24=48см