Геометрия: Надо найти x,y. заранее огромное всем;)

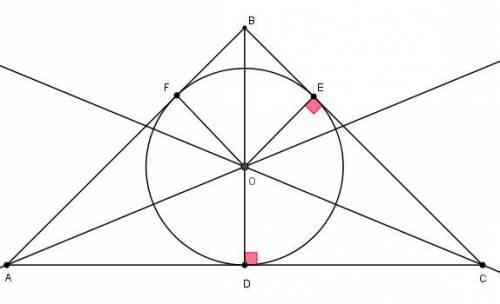
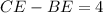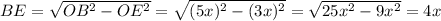
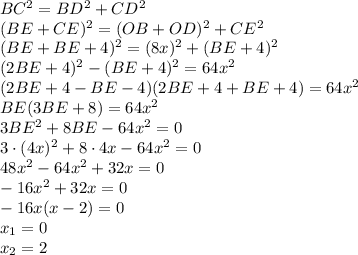
Точка пересечения биссектрис треугольника является центром вписанной в треугольник окружности и всегда находится внутри треугольника. Пусть OD = 3x и OB = 5x. CD = CE как касательные к окружности; OE = OD = 3x как радиусы, проведенные в точку касания.По условию . По т. Пифагора из треугольника BOEДалее из прямоугольного треугольника BDC по т. Пифагора:Первый корень не удовлетворяет условию, значит x = 2 см.Тогда BE = 4x = 8 см, значит CE = BE + 4 = 8 + 4 = 12 смCD = CE = 12 см, а так как BD является...

Надо найти x,y.
заранее огромное всем;)

Надо найти x,y. заранее огромное всем;)

👇

Увидеть ответ

Ответ:

Alla950

16.05.2021

Внимание :

Вы не указали у. Найдём за вами х и сторону , как предположительный у.

х=7

Сторона =2

Объяснение:

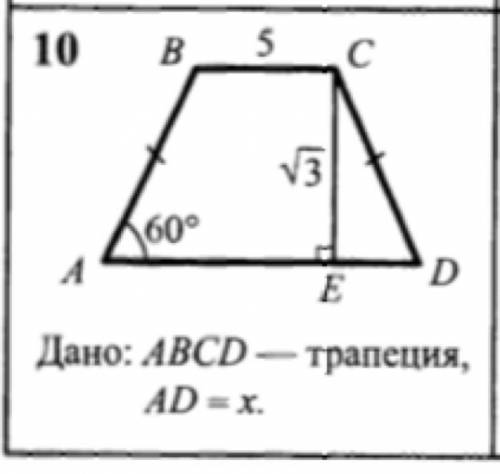
1)Тк трапеция равнобочная ( по условию рисунка), то угол А=углу Д = 60 градусов.

2) Треугольник СЕД - прямоугольный , тк СЕ - высота ( по усл рисунка) , тогда угол ЕСД=180-90-60=30.

3) катет против 30 градусов =1/2 гипотенузы ( запомнить, очень пригодится ).

Пусть боковая сторона трапеции=у, тогда по теореме Пифагора :

у^2=(sqrt 3)^2 +(у/2)^2

3/4 *у^2=3

у=2 сторона. Тогда ЕД = 2* 1/2=1.

4) опустим перпендикуляр ВО. Тогда ОЕ =ВС =5, и АО=ЕД =1.

Тогда АД= 1+5+1=7 ( тк треугольники равны по второму признаку УСУ)

если что-то не понятно, пишите в комментах. Успехов в учёбе! justDavid

4,8(95 оценок)

Открыть все ответы

Ответ:

paninadiana15

16.05.2021

Пусть ABCD – данный параллелограмм. Если он не является прямоугольником, то один из его углов A или B острый. Пусть для определенности A острый.
Опустим перпендикуляр AE из вершины A на прямую CB. Площадь трапеции AECD равна сумме площадей параллелограмма ABCD и треугольника AEB. Опустим перпендикуляр DF из вершины D на прямую CD. Тогда площадь трапеции AECD равна сумме площадей прямоугольника AEFD и треугольника DFC. Прямоугольные треугольники AEB и DFC равны, а значит, имеют равные площади. Отсюда следует, что площадь параллелограмма ABCD равна площади прямоугольника AEFD, т.е. равна AE • AD. Отрезок AE – высота параллелограмма, соответствующая стороне AD, и, следовательно, S = a • h. Теорема доказана.
Теорема о площади параллерограмма (докозательство)

Теорема о площади параллерограмма (докозательство)

4,6(4 оценок)

Ответ:

зайка583

16.05.2021

Точка пересечения биссектрис треугольника является центром вписанной в треугольник окружности и всегда находится внутри треугольника. Пусть OD = 3x и OB = 5x. CD = CE как касательные к окружности; OE = OD = 3x как радиусы, проведенные в точку касания.

По условию CE-BE=4 . По т. Пифагора из треугольника BOE

$BE=\sqrt{OB^2-OE^2}=\sqrt{(5x)^2-(3x)^2}=\sqrt{25x^2-9x^2}=4x$

Далее из прямоугольного треугольника BDC по т. Пифагора:

$BC^2=BD^2+CD^2\\ (BE+CE)^2=(OB+OD)^2+CE^2\\ (BE+BE+4)^2=(8x)^2+(BE+4)^2\\ (2BE+4)^2-(BE+4)^2=64x^2\\ (2BE+4-BE-4)(2BE+4+BE+4)=64x^2\\ BE(3BE+8)=64x^2\\ 3BE^2+8BE-64x^2=0\\ 3\cdot (4x)^2+8\cdot 4x-64x^2=0\\ 48x^2-64x^2+32x=0\\ -16x^2+32x=0\\ -16x(x-2)=0\\ x_1=0\\ x_2=2$