смотри в файле

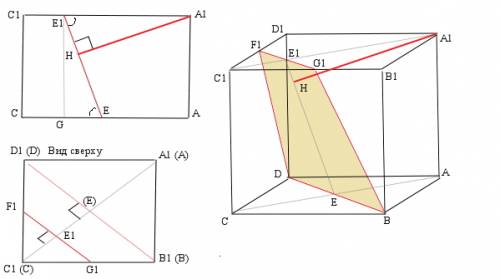
плоскость-сечение ---равнобокая трапеция BDF1G1
расстояние от точки до плоскости ---перпендикуляр => нужно построить плоскость, перпендикулярную трапеции...
это будет диагональное сечение куба A1ACC1 ---прямоугольник...
искомое расстояние А1Н
обозначим ребро куба (а)
треугольники A1E1H и EE1G подобны (они прямоугольные по построению,
углы A1E1H и GEE1 равны как накрестлежащие при параллельных прямых АС и А1С1 и секущей ЕЕ1) => А1Н / Е1G = А1Е1 / ЕЕ1
А1Н = Е1G * А1Е1 / ЕЕ1
Е1G = СС1 = а
А1Е1 = (3/4) * А1С1 (диагонали основания-квадрата перпендикулярны и точкой пересечения делятся пополам, треугольники D1B1C1 и F1G1C1 подобны с коэффициентом подобия 2 / 1 => С1Е1 = С1А1 / 4 )
по т.Пифагора А1С1 = а*V2
А1Е1 = 3а*V2 / 4
ЕЕ1 ---высота трапеции с бОльшим основанием = а*V2,
меньшим основанием = а*V2 / 2 (средняя линия треугольника D1B1C1),
боковой стороной = корень(a^2 + (a/2)^2) = a*V5 / 2 (по т.Пифагора)
по т.Пифагора ЕЕ1^2 = (a*V5 / 2)^2 - ((а*V2 - а*V2 / 2)/2)^2 = 5a^2 / 4 - a^2 / 8 = 9a^2 / 8
ЕЕ1 = 3а / (2*V2) = 3a*V2 / 4
получилось, что ЕЕ1 = А1Е1 =>
А1Н = E1G = а
A1H = 2
как-то так...
Цитата: "Правильная треугольная пирамида — это многогранник, у которого одна грань — основание пирамиды — правильный треугольник, а остальные — боковые грани — равные треугольники с общей вершиной. Высота опускается в центр основания из вершины. Только в правильном треугольнике совпадают точки пересечения медиан, биссектрис, высот, серединных перпендикуляров. Эта точка называется центром правильного треугольника. Центр правильного треугольника делит его высоты в отношении 2:1, считая от вершины."
Объем правильной треугольной пирамиды равен 1/3*Sосн*H, где Sосн - площадь правильного треугольника равная Sосн=(√3)а²/4 = (√3)16/4. = 4√3. H - высота пирамиды - перпендикуляр, опущенный из вершины пирамиды в центр основания.
Найдем высоту пирамиды.
Сначала найдем высоту основания по формуле h=(√3)a/2 = (√3)*4/2 = 2√3см.
Отрезок этой высоты от основания ребра до центра треугольника равна (2√3):3*2 =(4√3)/3см. Имеем прямоугольный треугольник, где гипотенуза - ребро пирамиды, один из катетов - высота пирамиды H, а другой катет - только чио найденный отрезок.
В этом тр-ке против угла 30 лежит катет, равный половине гипотенузы. Зная, что гипотенуза равна (8√3)/3, а катет равен (4√3)/3, по Пифагору находим второй катет (Н):
Н=√16 = 4см.
Искомый объем равен 1/3*Sосн*H = 1/3*(4√3)*4 =(16√3)/3 ≈ 9,24см³

Р abcd= 50 см. Паралелограма