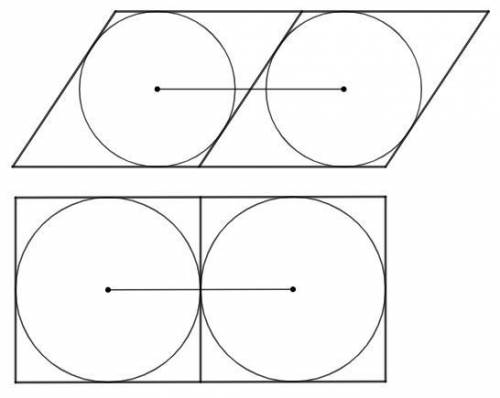
Окружности заключены между параллельными, следовательно их диаметры равны расстоянию между параллельными.
Окружности лежат внутри параллелограмма, следовательно заключены между большими сторонами.
Центры равноудалены от больших сторон => линия центров параллельна большим сторонам параллелограмма.
Данный параллелограмм можно разделить на два ромба.
В ромб можно вписать окружность.
Окружности касаются => внутренняя касательная перпендикулярна линии центров, а значит и большим сторонам параллелограмма.
Ромб с перпендикулярными сторонами - квадрат.
Искомая площадь равна двум квадратам со стороной x.
По теореме Пифагора x=4/√5
S =2*16/5 =6,4
24√10 см².
Объяснение:
По теореме
S = √(p•(p-a)(p-b)(p-c)) , где а, b, c - стороны треугольника, а р - его полупериметр
1) р = (14 + 14 + 12) : 2 = 20 (см);
2) S = √(20•(20-14)²(20-12)) = √(20•6²•8) = 6•4•√10 = 24√10 (см²).