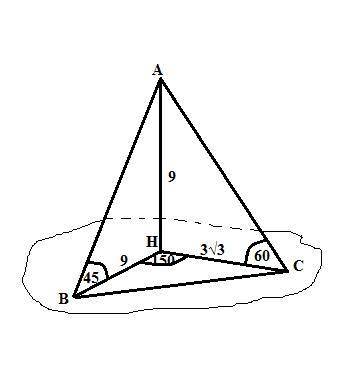
ВС = 3√21 см.
Объяснение:
Пусть основание перпендикуляра, опущенного на плоскость α - точка Н.
AH=9 см,<ABH=45°,<ACH=60°,<BHC=150°.
Заметим, что Cos150° = Cos(180 - 30) = -Cos30° = - √3/2.
В прямоугольном треугольнике АВН острые углы равны по 45°, треугольник равнобедренный и ВН=АН= 9см.
В прямоугольном треугольнике АСН тангенс угла С равен
Tg60 = √3 = AH/CH => CH = 9/√3 = 3√3 см.
В треугольнике ВНС по теореме косинусов:
BC²=BH²+CH²-2*BН*CH*cos150 = 81+27 - 2*9*3√3*(-√3/2) или
ВС² = 108+81 =189
BC = √189 = 3√21 см.
а) Пусть угол В равен х градусов, тогда угол А равен х/4 градусов (если в ... раз меньше, то надо разделить), а угол С равен (х - 90) градусов (если на ... меньше, то надо вычесть). Сумма углов треугольника равна (х + х/4 + (х - 90)) градусов или 180° ( по теореме о сумме углов треугольника). Составим уравнение и решим его.
х + х/4 + (х - 90) = 180;
х + 0,25х + х - 90 = 180;
2,25х - 90 = 180;
2,25х = 180 + 90;
2,25х = 270;
х = 270 : 2,25;
х = 120° - угол В;
х/4 = 120°/4 = 30° - угол А;
х - 90 = 120° - 90° = 30°.
ответ. ∠A = 30°; ∠B = 120°; ∠C = 30°.
б) Если в треугольнике два угла равны, то этот треугольник будет равнобедренным. Угол В равен 120°. Напротив этого угла лежит сторона АС, которая будет основанием. Две другие стороны треугольника АВ и ВС будут боковыми сторонами. Боковые стороны равнобедренного треугольника равны.
ответ. АВ = ВС.