30 см
Объяснение:
Рассмотрим вложение.
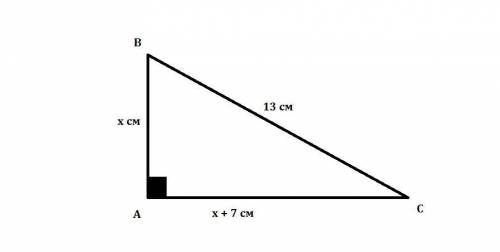
Нам дан ΔАВС: ∠А = 90°, ВС = 13 см
Пусть АВ = х см, тогда АС = х + 7 см. Воспользуемся т.Пифагора для нахождения стороны.
АВ² + АС² = ВС²
х² + (х + 7)² = 13²
х² + х² + 14х + 49 = 169
2х² + 14х + 49 - 169 = 0
2х² + 14х - 120 = 0 |:2
х² + 7х - 60 = 0
D = 7² - 4 * (-60) = 49 + 240 = 289 = 17²
x₁ = (-7 - 17)/2 = -24/2 = -12
x₂ = (-7 + 17)/2 = 10/2 = 5
т.к. сторона не может быть отрицательна, то АВ = 5 см, тогда
АС = 5 + 7 = 12 см
Чтобы найти периметр треугольника, надо сложить все стороны.
Р = АВ + ВС + АС = 5 + 13 + 12 = 30 см
Дано точки А (2; 4; -1), В (-1; 1; 3) і С (5; 1; 2). Знайдіть:1) координати векторів АВ, ВС;
AB = (-1-2; 1-4; 3-(-1)) = (-3; -3; 4).
BC = (5-(-1); 1-1; 2-3) = (6; 0; -1).
2) довжини(модулі) АВ, ВС;
|AB| = √((-3)² (-3)² + 4²) = √(9 + 9 + 16) = √34.
|BC| = √(6² + 0² + (-1) = √(36 + 0 + 1) = √37.
3) АВ+ВС = (-3; -3; 4) + (6; 0; -1) = (3; -3; 3).
АВ-ВС = (-3; -3; 4) - (6; 0; -1) = (-9; -3; 3).
4) 2АВ-½ВС = 2*(-3; -3; 4) – (1/2)* (6; 0; -1) =
= (-6; -6; 8) – (3; 0; (-1/2)) = (-9; -6; 8,5).
5) скалярний добуток векторів АВ і ВС;
АВ * ВС = (-3; -3; 4)* (6; 0; -1) = -18 + 0 – 4 = -22.
6) косинус кута між векторами АВ і ВС
cos(AB_BC) = -22/(√34*√37) = -22/√1258 = -11√1258/629,
7) визначити вид трикутника АВС.
Так как косинус угла В отрицателен, то угол В – тупой.
Треугольник АВС– тупоугольный.
В2В3= АВ4:4= 16:4=4 см.
Объяснение:
так как все кусочки А равны между собой и паралельны между собою со всеми В. За основною властивiстю паралельних прямих