1,5 (единиц)
Объяснение:
Дано:
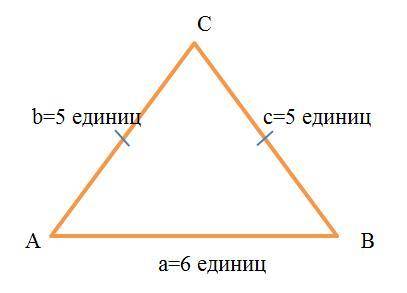
В ΔABC (см. рисунок)
a=AB = 6 (единиц) - основание
b = c = AC = BC = 5 (единиц) - равнобедренный
Найти: r - радиус вписанной окружности.
Решение.
Радиус вписанной окружности любого треугольника через его стороны a, b и c определяется по формуле:
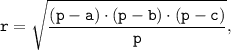
где p - полупериметр, то есть:
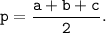
Так как b = c, то есть треугольник равнобедренный, то формула радиуса вписанной окружности превращается в вид:
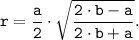
Отсюда, по заданным значениям сторон находим:
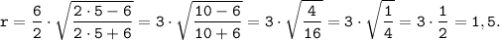
 , как диагонали равных квадратов, значит Δ
, как диагонали равных квадратов, значит Δ - равнобедренный, О - середина АС, значит
- равнобедренный, О - середина АС, значит  - медиана, биссектриса и высота, то есть
- медиана, биссектриса и высота, то есть  ⊥
⊥
 ⊥
⊥  ,
,  ⊥
⊥  , значит
, значит  ⊥
⊥  , и перпендикулярна любой прямой этой плоскости, в том числе
, и перпендикулярна любой прямой этой плоскости, в том числе  , значит ∠
, значит ∠
 ,
,  - проекция
- проекция  на плоскость АВС и
на плоскость АВС и  ⊥
⊥ , значит
, значит  ⊥
⊥ и ∠
и ∠

См. решение на рисунке