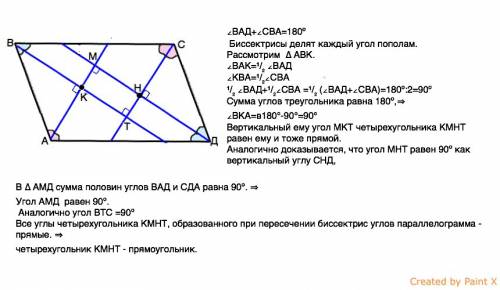
В параллелограмме противоположные углы равны по определению.
Так как противоположные стороны параллелограмма параллельны, то сумма его внутренних односторонних углов, как углов при параллельных прямых и секущей, равна 180º.
∠ВАД+∠СВА=180º
Биссектрисы параллелограмма делят каждый его угол пополам.
Рассмотрим ∆ АВК.
∠ВАК=¹/₂ ∠ВАД
∠КВА=¹/₂∠СВА
¹/₂ ∠ВАД+¹/₂∠СВА =¹/₂ (∠ВАД+∠СВА)=180º:2=90º
Сумма углов треугольника равна 180º,⇒
∠ВКА=в180°-90°=90°
Вертикальный ему угол МКТ четырехугольника КМНТ равен ему и тоже прямой.
Аналогично доказывается, что угол МНТ равен 90º как вертикальный углу СНД,
В ∆ АМД сумма половин внутренних односторонних углов ВАД и СДА равна 90º. ⇒
Угол АМД равен 90º.
Аналогично угол ВТС =90º
Все углы четырехугольника КМНТ, образованного при пересечении биссектрис углов параллелограмма - прямые. ⇒
четырехугольник КМНТ - прямоугольник.
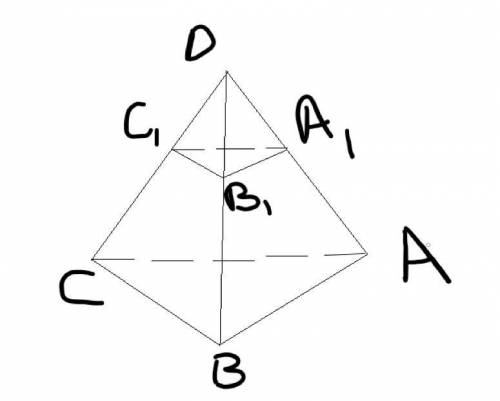
A1B1C1 || ABC, DA1 : AA1 = 3 : 4, S(A1B1C1)= 27 . Найти S(ABC)
Объяснение:
1) Т.к. плоскости граней A1B1C1 и ABC параллельны , то А1С1║АС⇒ соответственные углы ∠DC1A1=∠DCA и ∠D-общий . Поэтому ΔDC1A1 ∼ DCA по 2 углам .В подобных треугольниках сходственные стороны пропорциональны :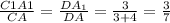 .
.
2) Т.к. A1B1C1 || ABC , то ΔA1B1C1 подобен ΔABC с коэффициентом
подобия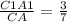 , к=
, к= 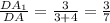 . По т. об отношении площадей подобных треугольников
. По т. об отношении площадей подобных треугольников
получаем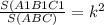 или
или 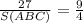 , S(ABC)=12 ед².
, S(ABC)=12 ед².