тк АВС-вписаный прямоугольный. то О-центр окр АО=ОВ
по тПифагора АВ=sqrt AC^2+BC^2 AB=13cm AO=R=6.5cm
S1(ABC) = 1/2 ab =30cm^2
S2( O) =π r^2 = 132.665cm^2
S2-S1= 102.665cm^2

Рассмотрю три решения:
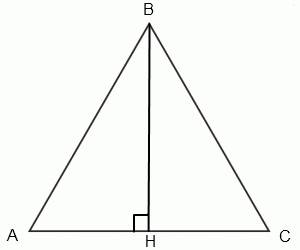
1) Пусть сторона AB = x, тогда AH = 0,5 * x, BH = 2 * (√3) ( по условию )
Тогда по теореме Пифагора: x ² = (0,5 * x) ² + (2 * (√3)) ²
x ² = (1/4 * x ²) + 4 * 3
x ² - (x ² / 4) = 12
(4 * x ² - x ²) / 4 = 12
3 * x ² = 48
x ² = 16
x = 4.
2) Треугольник ABH - прямоугольный, угол BAH = 60°.
sin 60° = BH / AB
AB = BH / sin 60°
AB = (2 * (√3)) / ((√3) / 2)
AB = 4.
3) Медианы в равностороннем треугольнике пересекаются в одной точке и делятся в соотношении 2:1 от вершины. 2/3 часть медианы будет являться радиусом описанной окружности. Значит R = (2 / 3) * 2 * (√3) = (4 * (√3)) / 3.
По теореме синусов:
2R = AB / sin 60°
(2 * 4 * (√3)) / 3 = AB / ((√3) / 2)
AB = (√3) / 2 * (8 * (√3) / 3)
AB = 4.
У прямоугольного треугольника центр описанной окружности лежит на середине гипотенузы.
Sтреугольника=5*12:2=30см^2
диаметр круга=гипотенузе треугольника
d^2=5^2+12^2=25+144=169
d=13см
R=13:2=6,5см
Sкруга=ПR^2=3,14*6,5^2=132,665см^2
Sкруга - Sтреугольника=132,665-30=102,665см^2