Question

Вцилиндр вписана правильная треугольная призма. площадь боковой поверхности призмы равна 5. найдите площадь боковой поверхности цилиндра.

Answer 1

Поскольку призма вписана в цилиндр то высоты обоих H одинаковы. Т. к. призма правильная, то площадь ее поверхности равна:
$S_{p} = 3aH \\$
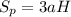
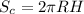
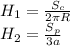
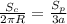
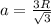
Далее площадь поверхности цилиндра равна:
$S_{c} = 2 \pi RH$
Поскольку у обоих одинаковые высоты, то мы можем приравнять их сначала выразив высоты обоих.:
$H_{1} = \frac{S_{c}}{2 \pi R} \\ H_{2} = \frac{S_{p}}{3a}$
Теперь приравняем их:
$\frac{S_{c}}{2 \pi R} = \frac{S_{p}}{3a}$
Далее для описанной окружности около треугольника (основая призмы) с радиусом R, длина стороны равна:
$a = \frac{3R}{\sqrt{3}}$
Теперь мы можем подставить это вместо "a" в нашем равенстве:

 $\frac{S_{c}}{2 \pi R} = \frac{S_{p}}{3*\frac{3R}{\sqrt{3}}} \\ \frac{S_{c}}{2 \pi R} = \frac{S_{p}*\sqrt{3}}{9R} \\ \frac{S_{c}}{2 \pi R} = \frac{5\sqrt{3}}{9R} \\ \frac{S_{c}}{2 \pi} = \frac{5\sqrt{3}}{9} \\ S_{c} = \frac{10 \pi\sqrt{3}}{9}$

Решал быстро, возможны ошибки :)