Пусть одна сторона-х,тогда вторая-(х+2) по теореме Пифагора x^+(x+2)^=10^ x^+x^+4x+4=100 2x^+4x-96=0 D=4^-4*2*(-96)=784 x1,2=-4+-28/2*2 x1=6 x2=-8(не может отриц.число быть решением),значит х=6-одна сторона 6+2=8-вторая сторона
Точка пересечения серединных перпендикуляров треугольника является центром окружности, описанной около этого треугольника. Так как данный треугольник — равнобедренный, то по теореме о медиане равнобедренного треугольника медиана, биссектриса и высота треугольника, проведенные к основанию, совпадают. Значит, высота совпадает с серединным перпендикуляром, проведенным к основанию треугольника. Следовательно, центр окружности, описанной около равнобедренного треугольника, лежит на медиане, проведенной к основанию.
Объяснение:
Теорема о 30-градусном угле такова: Катет, противолежащий углу 30-градусов в прямоугольном треугольнике — равен половине гипотенузы.
Тоесть катет BC — равен половине гипотенузы AB.
Но нам эта информация не в решении задачи, продолжим.
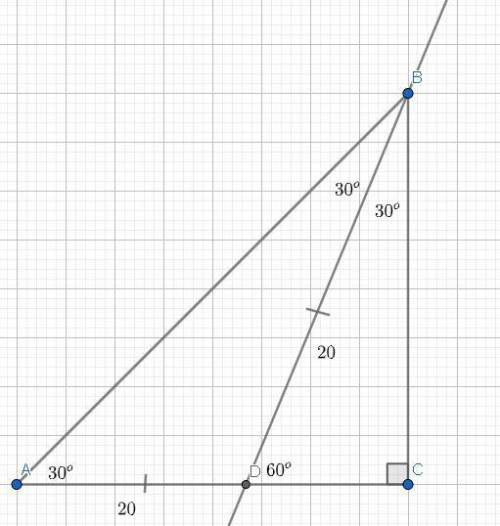
<B = <C - <A = 90-30 = 60°.
BD биссектриса — делит угол B — пополам, тоесть: <ABC == <DBC = 60/2 = 30°.
<A == <ABD = 30° => AD == DB; треугольник ABD — равнобедренный.
BD = 20 => AD == BD = 20.
<BDC = 30° => DC = DB/2 (теорема о 30-градусном угле прямоугольного треугольника).
DB = 20 => DC = 20/2 = 10
AD = 20; DC = 10 => AC = 10+20 = 30.
Вывод: AC = 30.
диагональ прям. делит его на 2 равных прям. тр-ка
пусть одна сторона прям. x, тогда вторая x+2
10²=x²+(x+2)²
100=x²+x²+4x+4
100=2(x²+2x+2)
50=x²+2x+2
x²+2x-48
x1=6
x2= -8 не может явл-ся решением < 0
6+2 = 8
стороны равны 6 и 8 см