В ромбе все стороны равны ⇒ AB = BC = CD = AD
ΔBAD - равнобедренный (AB = AD)
∠ABD = ∠ADB = (180° - ∠B)/2 = (180° - 60°)/2 = 120°/2 = 60°
Значит, ΔBAD - равносторонний ⇒ AB = AD = BD = 11 см
Периметр ромба ABCD равен:
Р = 4•BD = 4•11 = 44 см
ОТВЕТ: 44 см
Объяснение:
надеюсь не запутался
В данном случае необходимо использовать обратную теорему Пифагора. Которая гласит, что, если в треугольнике со сторонами a, b и c выполняется равенство c2 = a 2 + b 2 , то этот треугольник прямоугольный, причем прямой угол противолежит стороне c.
Так как сумма квадратов сторон треугольника МРК - MP и KP - равна квадрату большей стороны - MK:
9^2+12^2=15^2,значит треугольник-прямоугольный,то есть его площадь равна половине произведения катетов MPи KP:
S=9*12/2=54.
Если в треугольнике провести высоту PH, например, то она будет являться высотой и для треугольника МРК, и для треугольника КРТ. Таким образом, получаем, что:
Sкрт=1/2 * РН*КТ
Sмрк=1/2 * РН*МК
Данные площади относятся, как КТ/МК, то есть, как 10/15= 2/3 -> площадь треугольника КРТ равна 2*Sмрк /3 = 2* 54/3=36
Получается, что площадь второго треугольника - треугольника МРТ - равна 1/3 площади основного треугольника, то есть 18.
ответ: 18 и 36
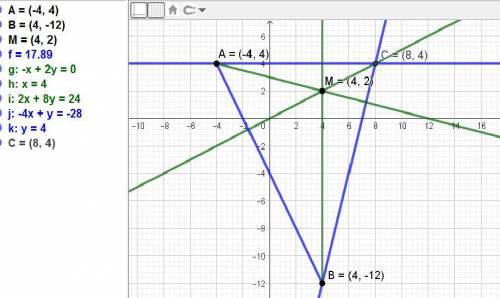
Вектор АМ = (4-(-4); 2-4) = (8; -2).
Уравнение высоты АМ:
х + 4)/8 = (у - 4)/(-2), или в общем виде х + 4у - 12 = 0.
Сторона треугольника АС перпендикулярна этой высоте.
Коэффициенты в уравнении ВС меняются так: -В и А, то есть -4 и 1.
Уравнение АВС: -4х + у + С = 0.
Для определения слагаемого С подставим координаты точки В:
-4*(-4) + (-12) + С = 0, отсюда С = 16 + 12 = 28.
Уравнение ВС: -4х + у + 28 = 0 или 4х - у - 28 = 0.
Так как сторона АС перпендикулярна высоте ВМ, у которой координаты точек по оси Ох совпадают, то АС - горизонтальная линия.
А так как она проходит через точку с ординатой у = 4, то это и есть уравнение стороны АС: у = 4.
Подставим у = 4 в уравнение ВС и найдём координату точки пересечения прямых, это точка С.
4х - 4 - 28 = 0, отсюда х = 32/4 = 8.
ответ: координаты точки С(8; 4).
44 см
Объяснение:
В ромбе все стороны равны, значит, P abcd = bd×4 = 11×4 = 44 см