На основании равнобедренного треугольника отметили две различные точки F и E , а на боковых сторонах AB и –BC точки D и G соответственно так, что AD +AE = AC и CF+ CG = AC. Найти угол между прямыми DF и EG, если угол ABC = 70°.
Объяснение:
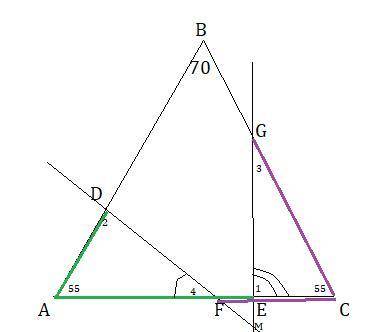
ΔАВС-равнобедренный,значит ∠А=∠В=(180°-70°):2=55°.
По условию АD+АЕ=АС и CF+ CG = AC ⇒АD=ЕС и AF=CG.
ΔADF ≈ΔCFG по 2 пропорциональным сторонам и равному углу между ними :∠А=∠В и AD/EC=AF/CG ⇒соответственные углы равны ∠1=∠2 ,∠3=∠4.
ΔFEM : найдем угол ∠М ; ∠Е=∠1, ∠F=∠4 . Сумма углов ∠F+∠Е=180°-55°=125° , тогда ∠М=180°-125°=55°
Объяснение:
Обозначим наш треугольник точками АВС, в котором угол В = 120°, так как сторона АВ = ВС следовательно угол А = С (свойства равнобедренных треугольников), а поскольку сумма углов треугольника равна 180°, тогда сумма углов А и С равняется 180-120=60, то есть А = С = 30°.
Проводим высоту ВD, которая образует прямоугольный треугольник АВD. Катет ВD лежит против угла 30°, значит равен половине гипотинузы АВ. ВD = 6/2 = 3. По теореме Пифагора находим второй катет АD.
АD = √(36-9)=√27=3√3
Так как в равнобедренном треугольнике высота является и медианой, тогда АС = АD + DС = 3√3 + 3√3 = 6√3
Периметр треугольника - это сумма всех сторон
Р = 6√3 + 6 + 6 = 6√3 + 12
ответ: 6√3 + 12
П.С. я вроде бы все понятно расписал, надеюсь, что рисунок сделаешь сам(а), если нет пиши в комментарии я сфоткаю, отправлю