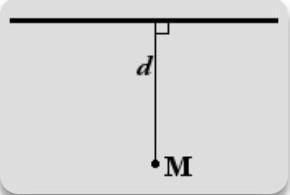
Определение. Расстояние от точки до прямой
равно длине перпендикуляра, опущенного из точки на прямую
Объяснение:
Если задано уравнение прямой Ax + By + C = 0, то расстояние от точки M(Mx, My) до прямой можно найти, используя следующую формулу
d = |A·Mx + B·My + C|
√A2 + B2
● Найти расстояние между прямой 3x + 4y - 6 = 0 и точкой M(-1, 3).
Решение. Подставим в формулу коэффициенты прямой и координаты точки
d = |3·(-1) + 4·3 - 6| = |-3 + 12 - 6| = |3| = 0.6
√32 + 42 √9 + 16 5
ответ: расстояние от точки до прямой равно 0.6.
думаю так;)
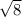 ответ:
ответ:
1. К
2. IV
3. 7 или -5
4. (0;0,5)
5. 2√73
6. (3√3; 1) или (-3√3; 1)
7. ромб
Объяснение:
1. Координаты точки К (3;0)
2. Координаты x>0, y<0 могут быть только в IV четверти
3. АВ=10= 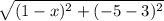 Приводим к квадратному уравнению
Приводим к квадратному уравнению 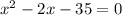 . Решаем через дискриминант и получаем х1=7, х2=(-5)
. Решаем через дискриминант и получаем х1=7, х2=(-5)
4. Координаты этой точки, допустим М (0;у) Нужно найти у. Поскольку эта точка М равноудалена от точек Д и Е, то расстояние между ними одинаковое, то есть по формуле расстояния между точками находим расстояния между ДМ и ЕМ и приравниваем. Решаем уравнение 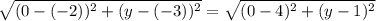 и получаем у=0,5
и получаем у=0,5
5. Координаты точек А(х;0), В(0;у) В формулу середины отрезка подставляем эти координаты и координаты точки М(-3;8): (-3)=(х+0)/2 х=(-6); 8=(0+у)/2 у=16. Теперь по формуле расстояния между точками находим расстояние между точками АВ и получаем АВ=2√73
6. Вершина В может быть или в 1й четверти, или во 2й четверти. По формуле расстояния между точками находим расстояние между точками А и С. Получаем 6. Поскольку ABC равносторонний треугольник, то АС=АВ=ВС=6. По формуле расстояния между точками находим расстояния между АВ и ВС и приравниваем. Решаем уравнение 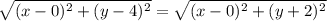 и получаем у=1.
и получаем у=1.
Подставляем значение у=1 в любую из сторон уравнения и получаем х1= 3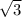 , х2= -3
, х2= -3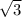
7. Если высчитать расстояние между точками, то есть стороны четырехугольника, то они равны: АВ=ВС=СД=АД=2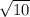 . То есть это либо ромб, либо квадрат. Дальше высчитываем длину диагоналей тоже как расстояние между точками: АС=2
. То есть это либо ромб, либо квадрат. Дальше высчитываем длину диагоналей тоже как расстояние между точками: АС=2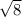 , ВД=4
, ВД=4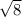 . То есть диагонали не равны, значит это не квадрат, а ромб.
. То есть диагонали не равны, значит это не квадрат, а ромб.
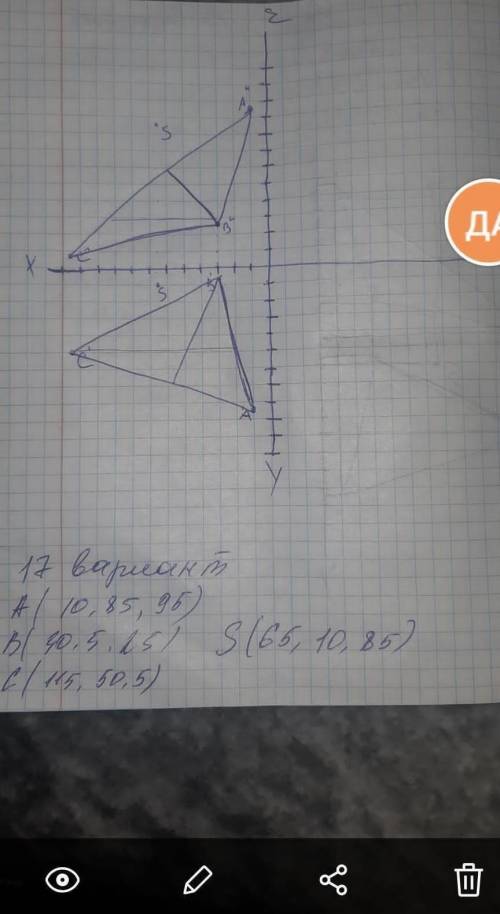
Ход решения
Через вершину B треугольника ABC проводим фронталь и горизонталь.
Переводим ABC в проецирующее положение. Для этого перпендикулярно В1Е1 вводим новую фронтальную плоскость Р4. Проецируем на неё точку S и треугольник ABC.
Из точки S4 проводим перпендикуляр к А4С4.
Длина отрезкаS4S – искомое расстояние между плоскостью треугольника ABC и точкой S.
Если требуется аналитическая проверка найденного расстояния, то по координатам точек А, В и С находим уравнение плоскости АВС:
95x -111y +154z - 6145 = 0.
Затем находим расстояние от точки S до плоскости АВС.
Для вычисления расстояния от точки S(Sx; Sy; Sz) до плоскости Ax + By + Cz + D = 0 используем формулу:
d = |A·Mx + B·My + C·Mz + D| /√(A² + B² + C²)
Подставим в формулу данные:
d = |95·65 + (-111)·10 + 154·85 + (-6145)| √(95² + (-111)² + 154²) = |6175 - 1110 + 13090 - 6145| /√(9025 + 12321 + 23716) =
= 12010 /√45062 = 6005√45062 /22531 ≈ 56.57672.
Полученное расчётное значение полностью совпадает с графическим расчётом.