
Это задание невыполнимо, так
как такого треугольника не су
ществует.
Объяснение:
Если боковая сторона 9см, то
основание равнобедренного
треугольника:
Р-2×9=38-18=20(см)
Длины сторон треугольника:
Основание - 20 см
1 боковая сторона - 9 см
2 боковая сторона - 9 см.
Треугольник скществует, если
сумма длин любых двух сто
рон треугольника больше
длины третьей стороны.
Проверим это условие:
1) 9+9=18 (см) сумма двух
боковых сторон;
18см<20см условие не выпол
няется.
Сумма длин двух боковых
сторон меньше длины осно
вания.
Отет:
Такой треугольник не сущест
вует.
Задача
Дано:
периметр равностороннего треугольника 18 см
периметр равнобедренного треугольника 20 см
Сторона равностороннего треугольника является основанием равнобедренного треугольника
Найти: стороны равнобедренного треугольника
Решение
1) 18:3=6 (см) - сторона равностороннего треугольника;
2) пусть боковые стороны равнобедренного треугольника равны х см, тогда
х +х + 6 = 20
2х=20-6
2х=14
х=7 (см) - боковые стороны равнобедренного треугольника;
ответ: стороны равнобедренного треугольника равны 6 см, 7 см и 7 см.
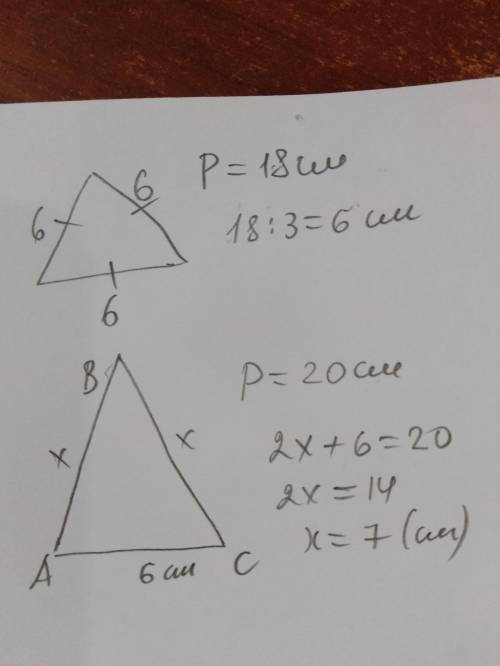
1. б
2. б и в
3. б
4. а
5. в
6. в
Объяснение:
1. б) может быть верно - свойство медианы равнобедренного треугольника, проведённой к основанию, а про медианы, проведённые к боковым сторонам, ничего подобного не говорится.
2. б) все его углы равны и в) любая высота является биссектрисой и медианой. б - свойство углов равностороннего треугольника, в - про это я пишу в 4 пункте
3. б) в равнобедренном. В любом точно нет. В равностороннем таких высот несколько, а спрашивается про одну
4. а) всегда верно - так как треугольник равносторонний, то у него стороны являются и основаниями и боковыми сторонами одновременно, если выделять здесь равнобедренные треугольники, поэтому свойство медианы равнобедренного треугольника распространяется на все медианы, биссектрисы и высоты.
5. в) ответы а и б неверны. ответ а неверен, так как основание равнобедренного треугольника не всегда равно боковым сторонам. ответ б неверен, так как медианой, биссектрисой и высотой является только медиана, ПРОВЕДЁННАЯ К ОСНОВАНИЮ (опять же таки повторяю про это свойство)
6. в) в равностороннем. Рассмотрим треугольник ABC, который не является ни равносторонним, ни равнобедренным и проведём в нём высоту. Высота AH не поделила т. ABC на равные треугольники ABH и ACH. Рассмотрим другой треугольник DEF, который является равнобедренным. В нём боковые стороны DE и FE. Высота EH делит треугольник на 2 равных. Они равны по 1, 2 и 3 признакам равенства треугольников (здесь можно доказать 1 из них, без разницы), так как EH является также медианой и биссектрисой, а FE=DE. А теперь проведём высоту FG. Она не поделила треугольник DEF на равные, так как высота проведена к боковой стороне, а не к основанию. Следовательно, вариант в верный.
P.S. учите геометрию и учитесь внимательно читать какие бы то ни было геометрические свойства, признаки, определения, теоремы и т.д. и т.п. и всё получится(: