Question

Задание 2 Найди неизвестные отрезки

Answer 1

$1) \ x = \sqrt{13} \\2) \ x = \sqrt{21} \\3) x_1 = 7, x_2=x_3 = 7\sqrt{2}$

Объяснение:

Обозначим неизвестные отрезки за x

1) неизвестный отрезок является гипотенузой прямоугольного треугольника:

$x = \sqrt{3^2+2^2} = \sqrt{9+4} = \sqrt{13}$

2) неизвестный отрезок является высотой, проведённой к основанию, в равнобедренном треугольнике. Как известно, высота, проведённая к основанию, в равнобедренном треугольнике является также медианой и биссектрисой. Следовательно неизвестный отрезок делит основание пополам и является катетом в прямоугольном треугольнике с гипотенузой равной 5 и катетом равным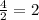 $\frac{4}{2} = 2$ :

$x = \sqrt{5^2 - 2^2} = \sqrt{25 - 4} = \sqrt{21}$

3) Здесь имеется три неизвестных отрезка, два из которых равны.

Начнём с высоты, опять же она проведена к основанию в равнобедренном треугольнике, а значит является и медианой и биссектрисой. А медиана проведённая к гипотенузе в прямоугольном треугольнике равна половине гипотенузы:

$x_1 = \frac{14}{2} = 7$

Нам известно, что оставшиеся неизвестные отрезки являются катетами в прямоугольном треугольнике и что они равны. Нам известна гипотенуза этого треугольника:

$x_2 = x_3,\\\sqrt{x_2^2+x_3^2} = 14 \\\sqrt{2x_2^2} = 14\\x_2\sqrt{2} = 14\\x_2 = \frac{14}{\sqrt{2} } = \frac{14\sqrt{2} }{2} = 7\sqrt{2}$