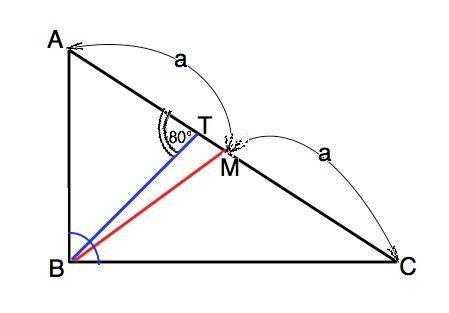
По условию ВМ=АМ=СМ, т.е. ВМ=АС:2. Если медиана треугольника равна половине стороны, к которой она проведена, то угол напротив этой стороны равен 90º. Следовательно, угол АВС=90°, и углы, на которые биссектриса ВТ делит его, равны 45°. Из суммы углов треугольника в ∆ АВТ угол А=180°-∠АТВ-∠АВТ=180°-80°-45°=55°. Из суммы углов треугольника АВС угол С=180°-90°-55°=35°
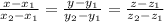
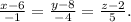
x-6 y-8 z-2
-1 -4 5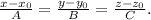
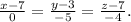
Необходимая для решения точка А3(2; 4; 7) задана по условию, а направляющий вектор для искомой прямой возьмём тот же, что для прямой А1А2, так как они параллельны: n=(-1;-4;5).
ответ: 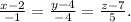
Здесь даже чертеж не нужен (хотя он для наглядности приложен)
Помним теорему синусов треугольника:
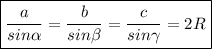
Где угол 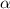 лежит напротив стороны
лежит напротив стороны  , угол
, угол 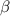 лежит напротив стороны
лежит напротив стороны 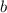 , а угол
, а угол 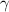 лежит напротив стороны
лежит напротив стороны  , а
, а 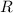 - радиус описанной около треугольника окружности (правда, окружность в этой задаче нам не нужна)
- радиус описанной около треугольника окружности (правда, окружность в этой задаче нам не нужна)
Учитывая, что 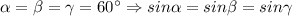
Но тогда теорему синусов можно переписать так:
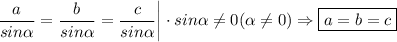
Что и требовалось доказать.
Можно ещё по-другому пойти.
Смотрим на рисунок. 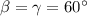 (нижние углы), то есть треугольник равнобедренный с основанием
(нижние углы), то есть треугольник равнобедренный с основанием  , значит, боковые стороны равны, то есть
, значит, боковые стороны равны, то есть 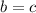
Далее, 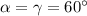 , то треугольник равнобедренный с основанием
, то треугольник равнобедренный с основанием 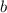 , боковые стороны равны, то есть
, боковые стороны равны, то есть 
Ну и завершающий вывод:
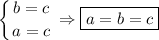
Что и требовалось доказать.
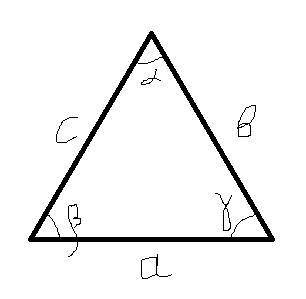
В треугольнике АВС медиана ВМ равна половине стороны АС (дано), следовательно, треугольник АВС - прямоугольный (<B = 90° по свойству медианы прямоугольного треугольника). Биссектриса ВТ прямого угла делит его на углы АВТ и ТВС, равные 45°. Угол АТВ равен 80° (дано). Это внешний угол треугольника ВТС и равен сумме двух внутренних углов, не смежных с ним, то есть <TBC+<BCT = <ATB или <BCT = 80° - 45° = 35°.
ответ: <C = 35°.