ответ: 40cm
Объяснение:
Пусть трапеция ABCD . Большее основание это AD=45 см.
боковые стороны АВ =20см, CD=15cm.
Пусть точка пересечения биссетрисс Т , и по условию задачи Т принадлежит основанию ВС.
Заметим что ∡TAD=∡ATB (накрест лежащие). Но ∡BAT=∡TAD, так как АТ - биссетриса.
Отсюда следует, что ∡BAT=∡BTA => ΔABT - равнобедренный.
То есть АВ=ВТ=20см.
По той же причине и треугольник СТD тоже равнобедренный,
ТС=CD=15 cm
Тогда ВС=ВТ+СТ=20+15=35 см
Тогда средняя линия трапеции MN=(AD+BC)/2=(45+35)/2= 40 cm
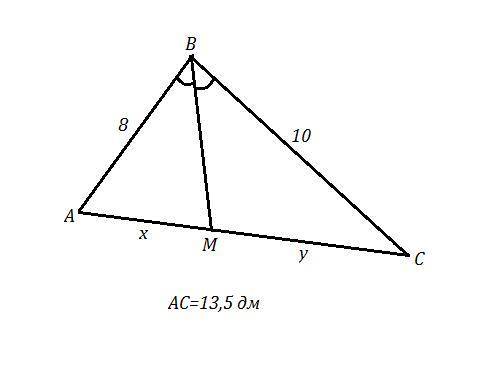
Стороны треугольника имеют длины : 8 дм , 10дм , 13,5 дм. Найти длины отрезков, на которые биссектриса большего угла делит противоположную сторону .
БОльший угол расположен против бОльшей стороны . Пусть бОльшая сторона АС=13,5 дм, тогда против неё лежит бОльший угол В .
ΔАВС , АВ=8 дм , ВС=10 дм , АС=13,5 дм . ВМ - биссектриса.
Обозначим АМ=х , СМ=у .
По свойству биссектрисы угла треугольника: 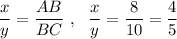 .
.
Тогда x=4k , y=5k ⇒ AC=AM+CM=x+y=4k+5k=9k , 9k=13,5 , k=1,5
AM=4k=4·1,5=6 дм
BC=5k=5·1,5=7,5 дм
Делим ромб диагоналями на 4 равных прямоугольных треугольника.Т.к диагонали делят углы ромба пополам то в этих треугольничках один из углов 60:2=30*.Катет лежащий против угла в 30 градусов равен половине гепотенузы (16:4=4) => половина меньшей диагонали 4:2=2 => вся меньшая диагональ 2*2=4 см.