
1) в равностороннем треугольнике все высоты равны.
Верно.Это свойство высот равностороннего треугольника
2)точка пересечения медиан произвольного треугольника - это центр окружности, описанной около этого треугольника.
Неверно. Центром описанной около треугольника окружности является точка пересечения серединных перпендикуляров к сторонам треугольника
4)медиана, это отрезок соеденяющий середины двух сторон треугольника.
Неверно. Медиана - отрезок, соединяющий вершину треугольника с серединой противоположной стороны
5) треугольник со сторонами 6,8,9- не существует.
Неверно. Существует.
Треугольник существует только тогда, когда сумма любых двух его сторон больше третьей.
Проверим:
6+8>9, 14>9
8+9>6, 17>6
6+9>8, 15>8
6) треугольник со сторонами 3,4,5 -прямоугольный.
Верно. Он египетский.
Египетский треугольник - прямоугольный треугольник с соотношением сторон 3:4:5
ответ 1 и 6
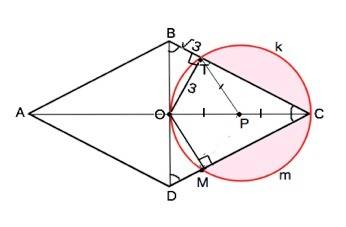
Площадь части круга, расположенной вне ромба, состоит из площади двух сегментов ТkC и DmC (см. рисунок в приложении).
ОС - диаметр, ТО=МО - высоты ромба, прямоугольные ∆ ОТС =∆ ОМС по катету и гипотенузе. ⇒ хорды ТС=МС⇒
сегменты ТkC и DmС равны.
В прямоугольном ∆ ОТВ тангенс угла ОВТ=ОТ:ВТ=3:√3=√3. Это тангенс 60° ⇒
в прямоугольном ∆ ВОС угол ВОС=30°
Диаметр ОС=ОТ:sin30°=6 см, радиус РС=РТ=3 см.
∆ ТРС равнобедренный, ∠ТРС=180°-2•30°=120°
Площадь сегмента ТkC равна разности между площадью сектора РТkC и площадью ∆ ТРС
Площадь сектора ТРС равна 1/3 площади круга=πr²:3=9π:3=3π, т.к. угол ТРС=1/3 градусной величины круга.
S ∆ТРС по формуле S=a•b•sina:2=9√3/4
S сегмента ТkC=3π - 9√3/4
Площадь 2-х таких сегментов 6π -9√3/2 см²
гегмн-и-үүьшгтгепнкеакау