ответ: 5√3см
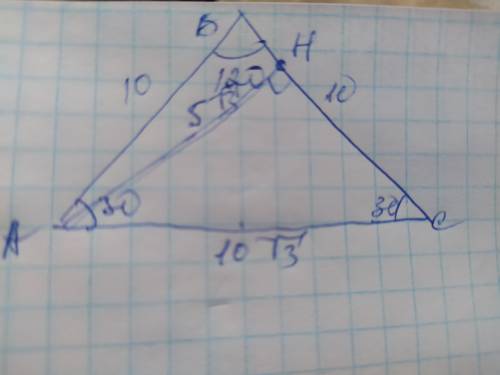
Объяснение: Обозначим вершины треугольника А В С, угол в=120°, а высоту АН. Сумма углов треугольника составляет 180°, поэтому можно найти угол С.
Угол С=180-120-3=30°. ∆АВС равнобедренный поскольку угол А= углу С, поэтому АВ=ВС=10см. Используя теорему косинусов найдём АС. АС²=АВ²+ВС²–2×АВ×ВС×cosB=
=10²+10²-2×10×10×cos120°=
=100+100-2×100×(-½)=200+100=300
AC=√300=√3×√100=10√3см
∆АСН. Он прямоугольный, где АН и СН катеты, а АС - гипотенуза. В прямоугольном треугольнике катет лежащий напротив угла 30° равен половине гипотенузы. Этим катетом является высота АН, поэтому АН=10√3÷2=5√3см
а)Так как АВ = ВС , то треугольник АВС - равнобедренный, ВТ - высота, значит медиана и биссектриса. (хотя в дано почему то не прописано, про ВТ) Треугольник АВТ - прямоугольный. Против угла 30 градусов лежит катет в 2 раза меньше гипотенузы, значит АВ=ВС = 4*2=8 см.
Сумма двух сторон треугольника больше третьей стороны (неравенство треугольника), значит в из треугольника АВС АС < АВ + ВС AC < 16см
из треугольника АВТ АВ <АТ + ВТ или АТ>АВ - ВТ АТ > 4 см => АС > 8 см
8см < АС < 16 см
б)Если провести отрезок из точки Т к середине АВ (например точке М) то он разделит АВ на отрезки равные по 4 см. То есть треугольник МВТ - равнобедренный и углы М и Т равны. Найдем их М =Т = (180-В):2=(180-60);2=60 - Значит треугольник МВТ - равносторонний, значит ТМ = 4 см, Аналогично можно доказать что отрезок ТК (К - середина ВС) тоже 4 см. Значит их сумма равна 8 см.
Объяснение:
У задачи решения.
если АВ перпендикулярна плоскости)
В этом случае необходимо найти АМ:
АМ:МВ = 2:3, АВ = АМ + МВ
=> 2х + 3х = 12,5
5х = 12,5
х = 2,5
АМ = 2х = 2 * 2,5 = 5 (м)
если АВ является наклонной к плоскости)
Необходимо найти расстояние от точки М до плоскости (длину отрезка МD).
Потребуются дополнительные построения: точка С, лежащая в плоскости; ВС - перпендикуляр к плоскости; АС - проекция наклонной АВ.
Треугольники АВС и АDМ подобны по первому признаку.
=> AM/AB = MD/BC, АВ = АМ + ВМ
MD = (12,5 * 2) / 5 = 5 (м)
Объяснение: