
Объяснение: квадрат диагонали параллелепипеда равен сумме квадратов его измерений:
Д²=дл²+шир²+выс²=
Д²=7²+6²+10²=49+36+100=185;
Д=√185см
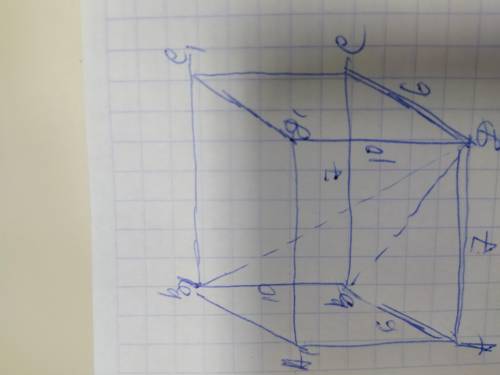
Если нужно найти диагонали граней параллелепипеда, тогда обозначим его вершины А В С Д В1 С1 Д1. Диагональ ВД делит грань АВСД на 2 равных прямоугольных треугольника, в которых стороны основания являются катетами а диагональ гипотенузой. Найдём диагональ ВД грани АВСД по теореме Пифагора: ВД²=АВ²+АД²=6²+7²=36+49=
=85; ВД=√85см. Такая же величина диагонали у грани А1В1С1Д1. Теперь найдём диагональ грани АА1ВВ1 также по теореме Пифагора:
АВ1²=АВ²+АА1²=6²+10²=36+100=136;
АВ1=√136=2√34см. Такая же величина диагонали у грани Д1ДС1С. Диагонали одной грани равны между собой.
Диагональ грани АА1ДД1=АД²+ДД1²=
=7²+10²=49+100=149; ДД1=√149см
Диагональ ДД1=√149см
2)б.
3)а.
4)в.
5)я прикрепила картинку к этому заданию.Не забудь написать «Дано: треугольникABC; a=7;b=8;c=5. Найти : <А-?» ответ , кстати , в конце <А=60 градусов.(просто не поместилось.)
6)AB=10x
S=pr
p=13x+13x+10x2=18x
S=p(p−13x)(p−13x)(p−10x)‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾√ — по формуле Герона.
приравниваем два равенства и находим х
10∗18x=p(p−13x)(p−13x)(p−10x)‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾√180x=18x∗5x∗5x∗8x‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾√
180x=60x2
x=3
AB=10x=30
ответ: 30
7) если СК биссектриса, то по ее свойству если СЕ/СВ=3:1 то и КЕ:ВК=3:1
Обозначим ВК=у, КЕ=3у значит, ВЕ=4у
т.к. угол ВОЕ центральный для угла С, то он=120 и тогда ∠ВОК=60
ВМ=ВО*sin 60
BM=8√3*√3/2=12 ВЕ=4у=24 ⇒ у=6 3у=3*6=18
8) 1. Теорема синусов для треугольника КОР KP/sin KOP=OP/sin OKP sin OKP=3*sqrt2*sqrt2/2/5=3/5 cos^2(OKP)=1-sin^2(OKP)=(4/5)^2 Т.к. КОР тупой, то ОКР острый, cos OKP=4/5
2. sin OPK=sin(180-KOP- OKP)=sin(KOP+OKP)=sin KOP*cos OKP+cos KOP*sin OKP sin OPK=sqrt2/2*(4/5-3/5)=sqrt2/10
3. S(KMP)=2*S(KOP)=OP*KP*sin OPK=3*sqrt2*5* sqrt2/10=3
9) Если диагонали трапеции перпендикулярны, то площадь можно найти по следующим формулам: S-Һв квадрате, где һ-высота или S-(a+b)в квадрате/4, где а иb -основания Воспользуемся последней формулой!Т к дана длина ср линии трапеции, то можно найти сумму длин оснований трапеци: ср линия3 1/2(а+b); 5%31/2(а+b); (а+b)-10см Найдем S- (а+b)в квадрате/4 %3D10в квадрате/ 4-25см2
10)в.