46.5. Искомая площадь вычисляется:
S=S₁-S₂-S₃,
S₁=π(AB)²/8; S₂=π(AD)²/8; S₃=π(DB)²/8.
S=π/8(AB²-AD²-DB²).
Подставим AB=AD+DB, CD²=AD*DB.
S=π/8(AD²+DB²+2AD*DB-AD²-DB²)=π*AD*DB/4 = π*CD²/4.
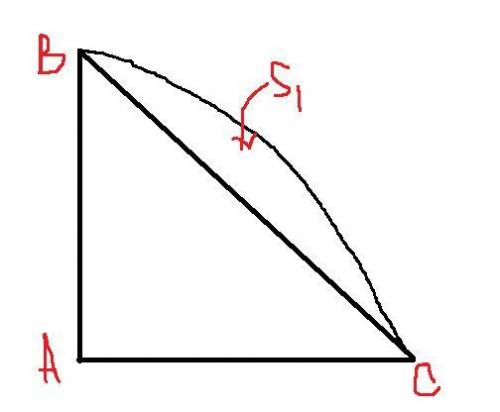
46.4. Рассмотрим четверть квадрата (Рис. ниже) со стороной a. Найдем S₁.
S₁=Sсек -Sтреуг, где Sсек - площадь сектора круга, ограниченного радиусами AB и AC, Sтреуг - площадь треугольника ABC.
Sсек = Sкр/4 = πa²/16.
Sтреуг = a²/8.
S₁ = a²/8*(π/2-1).
Искомая площадь: S=8*S₁ = a²*(π/2-1). По условию a=4 см.
S = 16(π/2-1) см.
46.6. Площадь (из задачи 46.5) вычисляется:
S=π*CD²/4 = π*AD*DB/4 = π*6*4/4 = 6π см².
Длина дуги окружности диаметра AB: L₁=πAB/2=5π см.
Длина дуги окружности диаметра AD: L₂=πAD/2=3π см.
Длина дуги окружности диаметра DB: L=πDB/2=2π см.
Периметр: L=L₁+L₂+L₃ = 5π+3π+2π = 10π см.
Пусть М - середина АВ, N - середина DC, тогда плоскость сечения проходит через М, N, D1, и, как не трудно увидеть, А1 (легко видеть, что в плоскости сечения есть прямая, параллельная А1D1 - это MN, и плоскость содержит одну точку этой прямой, то есть вся прямая A1D1 лежит в этой плоскости).
DN = а*корень(1 + (1/2)^2) = а*корень(5)/2;
Площадь сечения S = a^2*корень(5)/2, поэтому а = 2, V = 8.