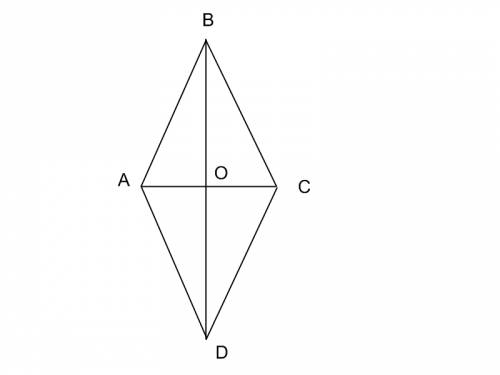
Дано: ABCD - ромб, BD=24см, AC=10см;
Найти: <A, <B, <C, <D;
Решение.
1) AB=BC=CD=AD, ВО=½BD, BO=12 и AO=½AC AO=5(по свойствам ромба), по теореме Пифагора AB²=BO²+AO², АВ²=12²+5², AB²=169, AB=13;
2)<A=<B=<C=<D, <ABO=<CBO, <BAO=<DAO(по свойствам ромба), sin ABO = AO/AB,
sin = 5/13, sin ABO≈0.38 <ABO≈68°, <BAO=180°-<BOA-<ABO, <BAO=180°-90°-68°=22°,
3) <A=44°, <B=136°, <C=44°, <D=136°
ответ: <A=44°, <B=136°, <C=44°, <D=136°.
ответ: Смотрите в объяснении.
Объяснение:
Можно ли любой отрезок выбрать в качестве единичного?Да. Единичный отрезок - отрезок, длина которого равна единице.
Чему равно расстояние между двумя совпадающими точками?Нулю (т.к. они совпадают, т.е. наложены друг на друга).
Какую точку называю серединой отрезка АВ?Точка, которая делит отрезок AB пополам, т.е. на 2 равных отрезка.