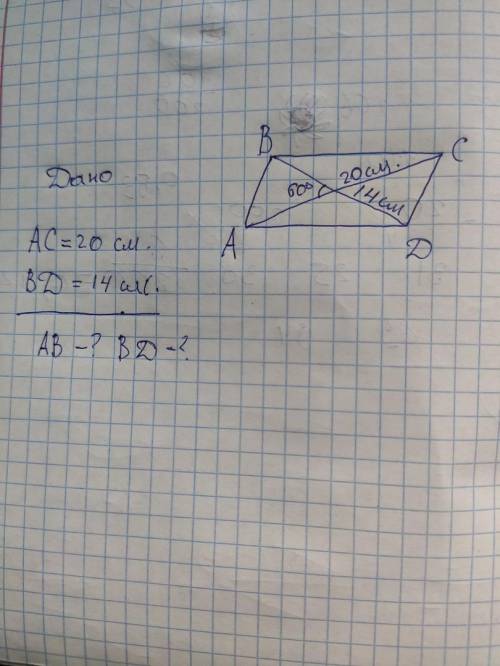
(Рисунок 2) Задача: Две параллельные прямые пересечены третьей. Известно, что разность двух внутренних односторонних углов равна 30°. Найти эти углы.
Решение:Углы 1 и 2 внутренние односторонние, их сумма равна 180градусов, т. е.
1∠ + ∠ 2 = 180градусов. (1)
Обозначим градусную меру угла 1 через х. По условию ∠ 2 - х = 30градусов, или ∠ 2 = 30градусов + x.
Подставим в равенство (1) значения углов 1 и 2, получим
х + 30градусов + х = 180градусов.
Решая это уравнение, получим х = 75градусов, т. е.
∠ 1 = 75градусов, a ∠ 2 = 180градусов - 75градусов = 105градусов.
Рисунок 1. Я просто нарисовала и нужно доказать параллельность KC и MQ.
Объяснение:
диагонали в параллелограмме в точке пересечения делятся пополам,значит ВО=OD=7,AO=OC=10
по теореме косинусов
АВ^2=BO^2+AO^2-2AO*BOcos60
AB=корень из 79
ВОА=60 значит ВОС=180-60=120
ВС^2=BO^2+OC^2-2BO*OCcos120
BC=корень из 219