а) Если прямая, пересекающая плоскость, перпендикулярна двум прямым в этой плоскости, проходящим через точку пересечения данной прямой и плоскости, то она перпендикулярна плоскости.
АС пересекает плоскость ВDО
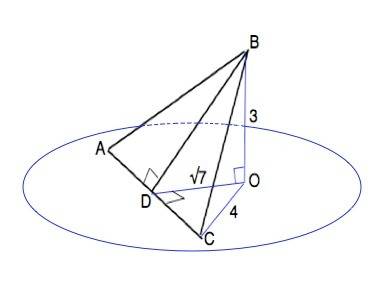
BD высота ∆ АВС. ⇒АС⊥ВD
Отрезок ОD- проекция ВD на плоскость альфа. По т. о 3-х перпендикулярах АС⊥ОD.
АС перпендикулярна двум прямым. проходащим через точку пересечения D прямой АС и плоскости ВDО. ⇒ АС⊥(ВDО)
б) ВО перпендикулярна плоскости альфа (дано).
Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
Плоскость ВСО проходит через прямую ВО, которая перпендикулярна плоскости альфа по условию. ⇒ Плоскость ВСО и альфа взаимно перпендикулярны.
в) Из ∆ ВОС Отношение катетов ВО:СО=3:4⇒
∆ ВОС египетский.⇒ Гипотенуза ВС=5 см
Из ∆ ОDC катет DC=√(OC²-OD*)=√(16-7)=3 см
∆ АВС равнобедренный (дано).⇒ ВD – высота и медиана. AD=CD⇒
АС=CD•2=6 см
Р=АВ+ВС+АС=16 см
5) 1 2+3=5 всего частей
2 25/5=5 состовляет одна часть
3 2*5=10 первая диагональ
4 3*5=15 вторая диагональ
5 (10 *15)/2= 75 см квадратных
1)21*15=315 см квадратных
2) 1 5*2=10 высота
2 (5*10)/2=25 см квадратных