пусть в трапеции АД и ВС основания, АД больше ВС. диагональ АС=АД, угол Д=72гр. значит угол АСД=72гр т. к. треугольник АСД равнобедренный. угол ВСД=180-72=108гр. угол ВСА=108-72=36гр. В треугольнике АВС угол В=108 гр угол ВСА=36 гр.
угол ВАС=180-(108+36)=36гр. В теугольнике два угла равны, значит он равнобедренный и АВ=ВС=СД
Можно решить сразу все три задания таким образом. Здесь речь идет о правильных многоугольниках, в заданиях спрашиваются длины, а не площади, значит отношения будут пропорциональны отношению сторон этих многоугольников. То есть у каждого задания один и тот же ответ. Не нужно вычислять радиусы вписанных и описанных окружностей, а также периметры. Достаточно вычислить отношения сторон.
12:8=1,5 - отношение (периметров, радиусов вписанной окружности, радиусов описанной окружности, нужное подчеркнуть) большого многоугольника к меньшему.
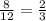 - отношение (периметра, радиуса вписанной окружности, радиуса описанной окружности, нужное подчеркнуть) меньшего многоугольника к большому.
- отношение (периметра, радиуса вписанной окружности, радиуса описанной окружности, нужное подчеркнуть) меньшего многоугольника к большому.
Т.к. AC=AD, то тр. ACD- равнобедренный и угол ADC=углу ACD=72.
угол A=углу D=72
угол CAD= 180-(72+72)=36, следовательно, угол BAC тоже 36
ВС и AD параллельны, а AC-секущая, значит угол BCA=углу CAD. Значит треуг. ABC-равнобедренный и AB=BC, ч.т.д.