ABC - р-б тр-к;BH - высота
1)тк ABC р-б треугольник по условию => BH является медианой и биссектриссой
2)AC (основание)=24 см;
BH - медиана (по доказанному);
из этого всего следует,что AH=HC=12см
3)тр-к ABH будет прямоугольным,тк BH - высота (по условию)
по теореме Пифагора AB^2=BH^2+AH^2
BH=35 см(по условию);AH=12 см (по доказанному),получим
AB^2=35^2+12^2
AB^2=1225+144
AB^2=1369
AB=37 см
ответ:37 см
* * * * * * * * * * * * * * * * * * * * * * * * *
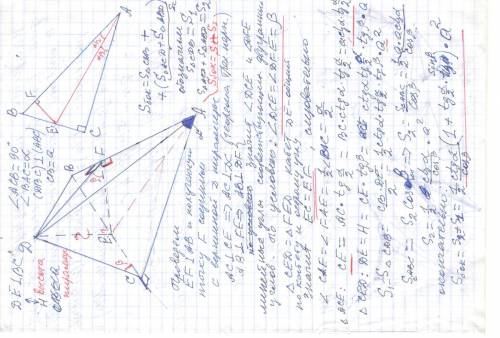
Основание пирамиды – прямоугольный треугольник с катетом а и противолежащим углом α. Боковая грань, содержащая данный катет, перпендикулярна плоскости основания, а две другие наклонены к ней под углом β. Найдите высоту (H) пирамиды и площадь боковой поверхности (Sбок).
Дано : ∠ACB =90° ; CB = a ;
( DCB) ⊥ (ABC) ; (DAC) ^ (ABC) = (DAB) ^ (ABC) = β
- - - - - - -
DE = H -? Sбок - ?
ответ : H=ctgα*tg(α/2)*tgβ , Sбок = 0,5*сtgα/cosβ (1+tg(α/2)*sinβ )*a²


Решение ........ во вложении
Высота равнобедренного треуг-ка делит данный треуг-к на 2 равных прямоугольных треугольника. Рассмотрим прямоуг. треугольник. Один катет=35см, другой равен 12 см (т.к. высота в р/б треуг-ке также является медианой). Боковая сторона треуг-ка есть гипоненуза и ее находим по теореме Пифагора с^2=35^2+12^2=1369 , c=37