1)Т.к. ромб является параллелограммом, то сумма углов прилежащих к стороне ромба равна 180 град., т.е. L A+ L B =180
L A = 180- L B = 180-120=60.
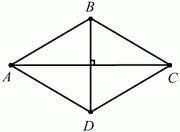
2) Построим диагональ ВD. ВD- биссектриса угла В ( св-во ромба),
тогда L CBD = L CDB =120/2=60.
Таким образом тр-к СВD-равносторонний , т.е. BD =ВС= a (! длина стороны ромба).
3) Из тр-ка ВСО- прям.: L ВСО = 60/2=30 град., тогда
СО =ВО* корень из 3 = а*корень из 3 ,значит
АС =2* СО=2* а*корень из 3 (! св-во пар-ма: диагонали точкой пересечения...).
ответ: 2* а*корень из 3; а.
Если обозначить за Х сторону основания нашей пирамиды, которое представляет собой равносторонний треугольник (т.к. пирамида правильная, и вершина проецируется в центр описанной окружности), то серединный перпендикуляр к стороне основания выразится как "корень квадратный из (x^2/3 - x^2/4)", или после преобразований x/(2 корня из3).
А высота пирамиды через радиус описанной возле основания окружности, выражающийся как X/(корень из 3), и через боковое ребро, которое согласно условию составляет 35 корней из 3, выразится так: "корень квадратный из (3675 - x^2/3)".
Отношение высоты пирамиды к серединному перпендикуляру даст выражение для тангенса угла между боковой гранью и плоскостью основания, который по условию равен 1,5. Записываем уравнение: слева - дробь,
числитель - корень квадратный из (3675 - x^2/3)
Знаменатель x/(2 корня из3)
Справа - 1,5.
Решая уравнение, находим: х = 84.
ответ: 84
Остались вопросы? Задавайте в личку!