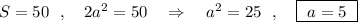№1 первый рисунок, на нем изображено то что дано.
Так как АВСD – параллелограмм, то АВ||CD, тогда угол DCN = угол
BNC как накрест-лежащие при паралельных прямых AB u CD и секущей CN.
CN – биссектриса по условию, значит угол DCN= угол BCN.
Исходя из равенств: угол BNC= угол DCN= угол BCN. Получим что ∆BNC – равнобедренный с основанием CN, так как углы при его основании равны.
У равнобедренного треугольника боковые стороны равны, следовательно BC=BN=4 см
Периметр параллелограмма это сумма двух его смежных сторон, умноженная на два. Тоесть:
P=(ВС+АВ)*2= (ВС+AN+BN)*2= (4+3+4)*2=22 см.
ответ: 22 см
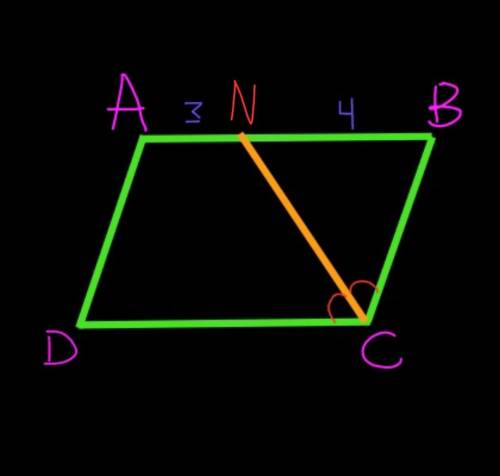
№2 второй рисунок, на нем изображено то что дано
Та что е ABCD – параллелограмм, то АD||BC, тогда угол DAM= угол BMA как накрест-лежащие при паралельных прямых AD и BC и секущей АМ.
АМ – по условию биссектриса, значит угол DAM= угол BAM.
Исходя из ранее найденного: угол DAM= угол АМВ= угол ВАМ.
Тогда получим что, ∆ВАМ – равнобедренный с основанием АМ, так как углы при основании равны.
АВ=ВМ как боковые стороны равнобедренного треугольника, тогда АВ=5 см.
Периметр параллелограмма это сумма двух его смежных сторон, умноженная на два. Тоесть:
Р=(АВ+ВС)*2=(АВ+ВМ+СМ)*2= (5+5+6)*2= 32 см.
ответ: 32 см
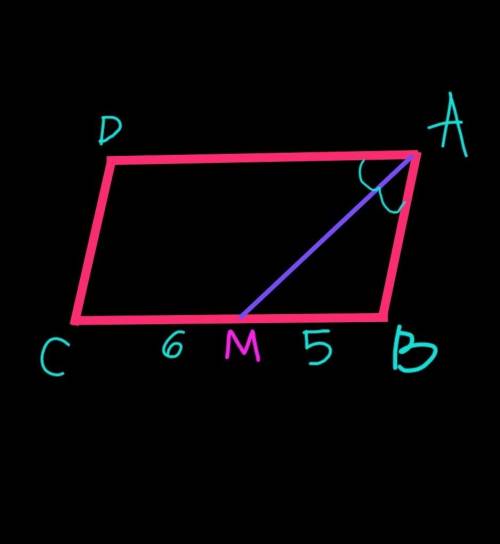
ответ: h=5 см .
АВСД - трапеция, АВ=СД , ∠А=∠Д=45° ,
ВС=а , ВН ⊥ АД , h=ВН=ВС=а , S(трап)=50см² .
Опусти перпендикуляр из вершины С на АД: СМ ⊥ АД .
Тогда ВСМН - прямоугольник , противоположные стороны которого равны, ВС=МН и ВН=СМ , но так как по условию ВС=ВН, то ВСМН - квадрат, сторону которого обозначим "а" .
ΔАВН - прямоугольный, с углом ∠А=45° . Тогда и ∠АВН=90°-45°=45° .
То есть ΔАВН - равнобедренный и АН=ВН=а .
Аналогично, из ΔСДМ получаем, что ДМ=СМ=а .
Тогда АД=АН+НМ+МД=а+а+а=3а .
Площадь трапеции :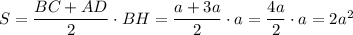
По условию: