Начнем с плоскости сечения шара. Смотрим на нее как бы сверху - видим круг.
Соединим концы хорды, стягивающей угол 120градусов, и ее середину с центром окружности, ограничивающей плоскость сечения.
Получим прямоугольный треугольник с острым углом 30 градусов, против которого лежит катет, равный √5
Радиус r, как гипотенуза этого треугольника, равен 2√5
Теперь представим себе сечение, которое проходит перпендикулярно плоскости данного сечения.
Диаметр сечения, которое нам было дано, является теперь хордой, расстояние от центра которой до центра шара равно 4 см. Рассмотрим треугольник, который получится, когда мы соединим центр шара и конец этой хорды.
Радиус R шара здесь - гипотенуза прямоугольного треугольника, катеты которого нам известны.
R²= (2√5)²+4²=20+16=36
R=√36=6 cм
Площадь поверхности сферы равна учетверенной площади большого круга:
S=4 π R²
S=4 π *36=144 см²
Объем шара в полтора раза меньше, чем объем описанного вокруг него цилиндра.
V=4/3 π R³
V=4π216:3=288π см³
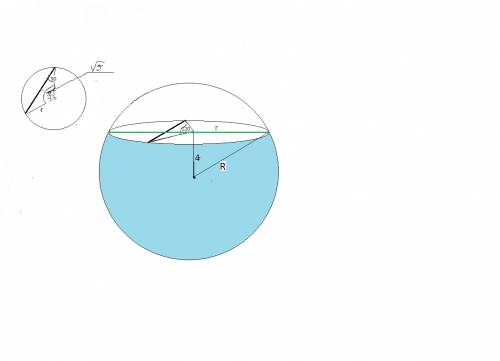
Изобразим круг, который является сечением шара. В нем покажем центр сечения О1, хорду АВ, отрезок О1Д, являющийся расстоянием от О1 до хорды АВ,. Хорда стягивает угол в 120⁰, значит, центральный угол АО1В равен 120⁰. О1Д делит хорду пополам.
Рассмотрим прямоугольный ΔАДО1. В нём угол АДО1 = 90⁰, угол ДО1А = 120⁰:2 = 60⁰, т.к высота равнобедренного ΔАО1В является и биссектрисой. ОА = r - радиус рассматриваемого кругового сечения является гипотенузой в ΔАДО1.
АО1 = ДО1: cos 60⁰ = √5: 0,5 = 2√5(см).
Осталось найти радиус шара.
Изобразим шар с центром в точке О, расстояние ОО1 до сечения задано (ОО1 = 4 см) проведём след сечения - прямую АО1В параллельную диаметру шара. Рассмотрим прямоугольный ΔАОО1, в котором биссектрисой является радиус шара R=АО, катетами ОО1 = 4см и АО1 = 2√5см.
Используем иеорему Пифагора: R = √(4² +(2√5)²) = √(16 +20) = √36 = 6(см)
Объём шара вычисляется по формуле
V = 4π·R³/3 = 4π·6³/3 = 288π(см³)
Площадь поверхности шара вычислим
S = 4π·R² = 4π·6² = 144π(см²)