3. Основание прямоугольного параллелепипеда ABCDA,B,C,D, - квадрат со стороной 6 см. точки К и P - точки пересечения диагоналей граней AA1D1D и CDD1C1 соответственно. Найдите,
Во сколько раз сторона KD, треугольника PKD1 больше стороны
PK, если длина бокового ребра параллелепипеда равна 8 см.
Ребят очень нужна
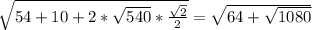
Площадь основания=4√3
Sоснования =a²√3/4, а- длина ребра основания
а²√3/4=4√3 > a=4 - ребро основания
Площадь боковой поверхности=16√3-4√3=12√3
S бок =Роснования*h/2 (h- анофема или высота боковой грани)
Роснования=3*а=3*4=12
12√3=12*h/2 > h=2√3 - высота боковой грани
Так как боковые грани равны между собой и есть равнобедренные треугольники, то h - и высота и медиана
Пусть b - боковое ребро, тогда по теореме Пифагора:
b=√(h²+(a/2)²)=√(4*3+4)=√16 =4 - боковое ребро
V=Sоснования*H/3 H - высота пирамиды
R=a/√3 - радиус описанной окружности основания ( равностороннего треугольника) R=4/√3
H=√(b²-R²)=√(16-16/3)=4√(1-1/3)=4√2 / √3
V=4√3 *4√2 /√3=16√2
ответ боковое ребро=4
объём=16√3
Sбок =12√3