При центральной симметрии отрезок отображается в равный и параллельный ему отрезок.
Стороны шестиугольника А₁А₂ и А₄А₅ равны и параллельны, значит эти отрезки центрально-симметричны. Центр симметрии - точка пересечения отрезков А₁А₄ и А₂А₅ - точка О. По определению центральной симметрии точка О - середина этих отрезков.
Аналогично, отрезки А₂А₃ и А₅А₆ центрально-симметричны относительно точки пересечения отрезков А₂А₅ и А₃А₆, которая является их серединой. Но середина отрезка А₂А₅ - точка О, значит точка О и середина отрезка А₃А₆. Итак, все диагонали пересекаются в одной точке.
253,5см²
Объяснение:
Дано
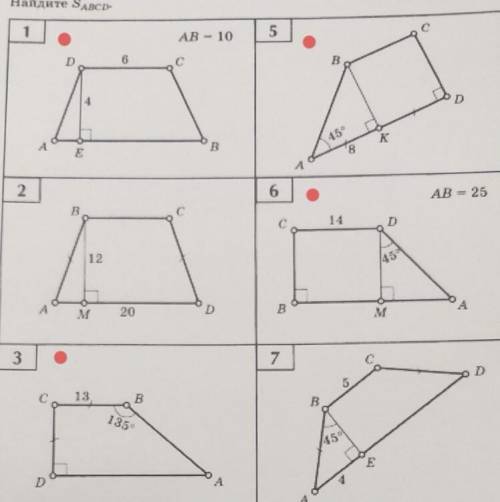
ABCD- трапеция
СВ=CD=13см
<CBA=135°
S=?
Решение
Проведём высоту ВК.
<СВА=135°, по условию.
Сумма углов прилежащих к боковой стороне трапеции равна 180°
<СВА+<ВАD=180° (свойство трапеции)
<ВАD=180°-135°=45°
∆ВКА- прямоугольный, равнобедренный
(Углы <ВКА=90°; <ВАК=45°; <КВА=45°). ВК=КА
СВКD- квадрат.
СВ=ВК=DK=CD=13 см
КА=13см
S=BK(CD+DA)/2=13(13+13+13)/2=13*39/2=
=253,5см²