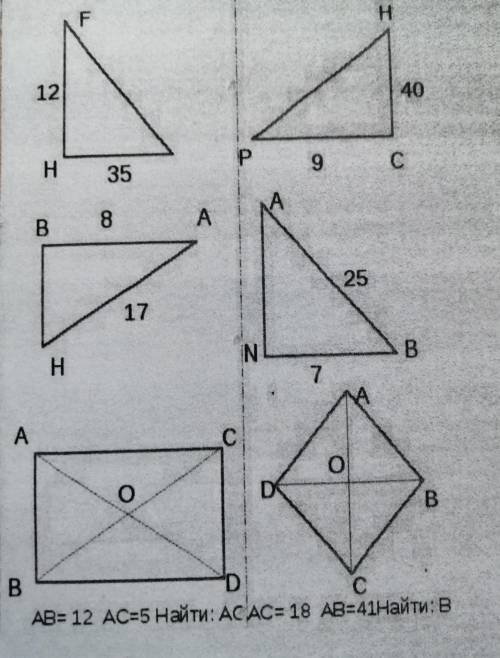
Задание №1
Объяснение:
Пирамида SABCD. Апофема SH - высота треугольника SAB. O - точка пересечения диагоналей основания, SO - высота пирамиды.
1) Рассмотрим прямоугольный треугольник OHS. По теореме пифагора:
OH² = SH² - SO²
OH² = 4a² - 3a²
OH = a
По теореме Фалеса: BC = 2OH = 2a
Сторона основания 2a
2) SHO - линейный угол двугранного угла SABO. Найдя его, найдем и SABO, следовательно угол между боковой гранью и основанием.
Из прямоугольного треугольника SHO:
sin<SHO = SO/SH
sin<SHO = a√3/2a = √3/2
<SHO = 60°
Угол между боковой гранью и основанием 60°
3) S = Sбок + Sосн
В основании квадрат, значит Sосн = AB² = (2a)² = 4a²
Sбок = Pосн*SH/2
Pосн = 4*2a = 8a
Sбок = 8a*2a/2 = 8a²
S = 8a² + 4a² = 12a²
Площадь 12а²
4) Из точки О (это и есть центр основания) проводим перпендикуляр к апофеме SH, обозначаем H1. SH1 - расстояние от центра основания до плоскости боковой грани.
Из прямоугольного треугольника OH1H:
sin<SHO = OH1/OH
но sin<SHO = √3/2
√3/2 = OH1/a
OH1 = a√3/2
ответы: a; 60°; 12а²; a√3/2
1. 37
2. 41
3. 15
4. 24
5. CD = 12; BD = 5; BC = 13; AD = 13; AO = 6,5; DO = 6,5; BO = 6,5; CO = 6,5
Объяснение:
Сумма квадратных катетов равна квадратной гипотенузе.
1. 12^2 + 35^2 = 144 + 1225 = 1369
ответ: 37
2. 40^2 + 9^2 = 1600 + 81 = 1681
ответ: 41
3. 8^2 + x^2 = 17^2
64 + x^2 = 289
x^2 = 289 - 64
x^2 = 225
x =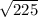
x = 15
ответ: 15
4. 7^2 + x^2 = 25^2
49 + x^2 = 625
x^2 = 625 - 49
x^2 = 576
x =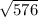
x = 24
ответ: 24
5. BC = 12^2 + 5^2 = 144 + 25 = 169
Так как ABCD - параллелограмм, то CD = AB = 12; BD = AC = 5; AD = BC = 13.
AO = DO = BO = CO = 13 / 2 = 6,5
ответ: CD = 12; BD = 5; BC = 13; AD = 13; AO = 6,5; DO = 6,5; BO = 6,5; CO = 6,5