-- Дано : уголABC и уголHKP,AB = HK,AC = HP,угол A = углу (?) Доказать : уголABC = угол (?) Доказательство : 1)по условию теоремы уголA = углуH,поэтому треугольник ABC можно наложить на треугольник (?) так,что вершина A совместится с вершиной H,а стороны AB и AC наложатся соответственно на лучи HK и (?) 2) По условию AB= (?),AC = (?),следовательно,сторона AB совместится со стороной (?),а сторона AC - со стороной (?),в частности,совместятся точки B и (?),C и (?).Поэтому совместятся стороны (?) и (?). 3)Итак,треугольники ABC и HKP полностью совместятся,значит,они (?). Теорема доказана вставте нужные слова вместо "(?)".
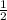АС=[tex] \frac{1}{2} *6=3 см;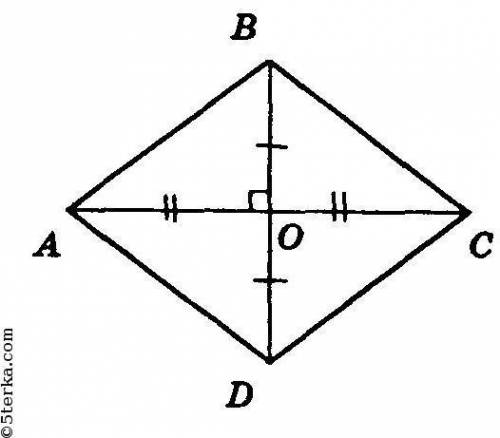
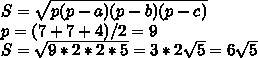
2)b= √(64-9)= √55
3) получаются 4 равных прямоугольных треугольника. а= 3 в= 4 . значит по с √(16+9)= 5
4)d= √(25+16)=√41
5)h= √(49-4)= √45. a= 4. S= 1/2*a*h(a)= 1/2*4*√45= 2√45
ответ S= 2√45
6)берем основания трапеции . 14-6= 8 .
из за того что трапеция равнобокая , то сторона маленького треугольника равна 8/2= 4
по теореме Пифагора . боковая сторона трапеции это гипотенуза , а катет = 4 .
высота трапеции будет равна 2 катету треугольника . h=√(25-16)=3
ответ высота трапеции равна 3