6 см
Объяснение:
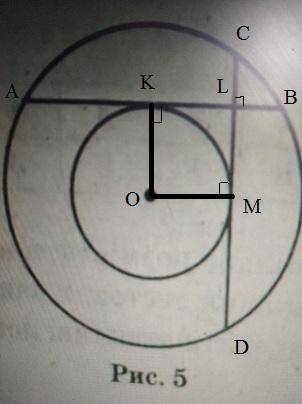
Радиусы OK и ОМ, проведённые в точки касания хорд с малой окружностью, будут перпендикулярны касательным - хордам АВ и CD. Но также, по свойству диаметра, перпендикулярного хорде, точки К и М будут лежать на серединах отрезков АВ и CD.
АВ=CD=AL+LB=16+4=20см
AK=KB=20/2=10см
KL=KB-LB=10-4=6см
KLMO - квадрат, поскольку все его смежные стороны имеют между собой прямой угол (2 - как радиусы к касательным, 1 - по условию перпендикулярности хорд, и оставшийся тоже получается 90°), и две его смежные стороны ОК и ОМ равны радиусу.
Значит ОМ=KL=6см
ответ:1. Если KM = NJ, ML = JR, __М= J__, то ΔKML=ΔNJR по первому признаку- по двум сторонам и углу между ними
2. KM = NJ, ML = JR,_KL=NR_, то ΔKML=ΔNJR по третьему признаку-по трем сторонам.
3. KL = NR, ∡ K = ∡ N, _∡ L= ∡ R, то
ΔKML=ΔNJR по второму признаку-по стороне и двум прилежащим углам.
4. KL = NR, ∡ K = ∡ N,_KM=NJ__ , то ΔKML=ΔNJR по первому признаку- по двум сторонам и углу между ними
5. ∡ M = ∡ J, ∡ L = ∡ R, _ML =NR_ , то ΔKML=ΔNJR по второму признаку-по стороне и двум прилежащим углам.
Если осевое сечение цилиндра представляет собой квадрат, то высота цилиндра равна диаметру его основания, или двум его радиусам.
Площадь основания (круга) равна п*r^2, откуда радиус основания равен 4.
А его диаметр (соответственно, и высота цилиндра) - вдвое больше, т.е. 8.
Площадь поковой поверхности равна произведению длины окружности основания, которая при радиусе 4 равна 8п, на высоту, т.е. 64п квадратных единиц, в нашем случае - сантиметров.