класс геометрия 1) Параллелограммом называется *
• четырёхугольник, стороны которого равны
• четырёхугольник, стороны которого попарно параллельны
• четырёхугольник, стороны которого параллельны и равны
• четырёхугольник, стороны которого параллельны
2) Прямоугольником называется *
• параллелограмм, у которого все углы равны
• четырёхугольник, все углы которого равны
• четырёхугольник, у которого все углы прямые
• параллелограмм, у которого все углы прямые
3) Ромбом называется *
• четырёхугольник, стороны которого равны
• параллелограмм, стороны которого равны
• параллелограмм, у которого все углы прямые
• параллелограмм, у которого диагонали равны
4) У прямоугольника *
• диагонали взаимно перпендикулярны
• диагонали равны
• диагонали являются биссектрисами углов
• стороны равны
5) У ромба *
• диагонали взаимно перпендикулярны
• диагонали равны
• диагонали являются биссектрисами углов
• углы, прилежащие к одной стороне равны
6) Квадратом называется *
• четырёхугольник, у которого все углы равны
• прямоугольник, у которого все стороны равны
• ромб, у которого все углы прямые
• параллелограмм, у которого все стороны равны
7) У квадрата *
• диагонали взаимно перпендикулярны
• диагонали равны
• диагонали являются биссектрисами углов
•.противоположные углы равны
8) Если у четырёхугольника *
• две стороны параллельны и равны, то он параллелограмм
• диагонали равны, то он параллелограмм
• диагонали равны, то он прямоугольник
• стороны равны, то он прямоугольник
9) Если у параллелограмма *
• диагонали равны, то он прямоугольник
• диагонали взаимно перпендикулярны, то он ромб
• стороны равны, то он прямоугольник
• диагонали равны, то он ромб
10) Трапеция это *
• четырёхугольник, у которого стороны параллельны
• Четырёхугольник, у которого две стороны параллельны, а две другие нет
• параллелограмм, у которого стороны равны
• четырёхугольник, у которого есть прямой угол
11) Если у трапеции *
• две стороны равны, то она равнобокая
• все стороны равны, то она равнобокая
• диагонали равны, то она равнобокая
• углы при основании равны, то она равнобокая
12) Если у трапеции *
• есть прямой угол, то она равнобокая
• есть прямой угол, то она прямоугольная
• есть угол 30 градусов, то она прямоугольная • диагонали равны, то она прямоугольная
234
Объяснение:
Допустим дана трапеция ABCD, угол ВАС - прямой, биссектриса проведена из угла CDA, АВ=12см, CD=15см. Т.к. биссектриса делит угол пополам, то угол СDB равен углу BDA.
Угол BDA равен углу DBC как накрестлежащий. Следовательно CDB=BDA=DBC. Значит треугольник DBC - равнобедренный и сторона CD равна стороне BC, значит BC=15 см.
Проведем высоту СН к основанию AD. Т.к. трапеция прямоугольная CH=AD=12см. У нас получился прямоугольный треугольник CHD, в котором известно CH=12см, CD=15см.
Нужно найти катет HD.
Используем формулу для нахождения гипотенузы в прямоугольном треугольнике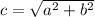
Т.к. ABCH - прямоугольник, то ВС=АH=15см. Из этого следует, что AD=15+9=24. Т.к. трапеция прямоугольная, то сторона AB - высота.
Найдем площадь трапеции по формуле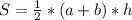
S=1/2*(15+24)*12=6*39=234