
Объединение монгольских племён
Объяснение:
В начале XIII в. в Центральной Азии возникло новое государство - Монгольская империя. Объединение монгольских племен в немалой степени было вызвано изменением климатических условий местности, где проживали монголы. XI и XII вв. были благоприятными для монголов. Длительный период влажных лет в восточной степи привел к тому, что умножились стада, а, следовательно, одна и та же территория могла прокормить больше людей. Произошло увеличение населения в Монголии. Однако в конце XII в. климат стал постепенно меняться в сторону ухудшения, стал более засушливым. Кочевое скотоводство стало малопродуктивным, в степи стало много избыточного населения. Началась обычная в таких условиях борьба с соседями за пастбища, а также вторжения на земли соседей-земледельцев.
Огромную роль в создании Монгольской империи сыграл Темуджин. Железная воля, властолюбие и целеустремленность позволили Темуджину собрать монголов в единое политическое целое и спаять общество на основе т. н. закона Чингисхана - Яссы. На съезде монгольской знати (курултае) в 1206 г. создатель империи Темуджин (Темучин) был провозглашен великим ханом всех монголов и принял имя Чингисхан.
Объяснение:
Найдём критические точки (это те значения в которых производная функции равна нулю или не имеет значений (к примеру 1/x, при x=0 функция не имеет значения), они называются точками разрыва).
Сразу видно что у функции нет точек разрыва (то есть она определена на всей числовой прямой), поэтому просто приравняем производную функции к нулю:
[Производная степенной функции: 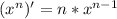 ]
]
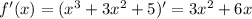
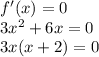
Произведение равно нулю, когда хотя бы один из множителей равен нулю:
3x=0 или x+2=0
x=0 или x=-2
Итого у нас 2 точки экстремума.
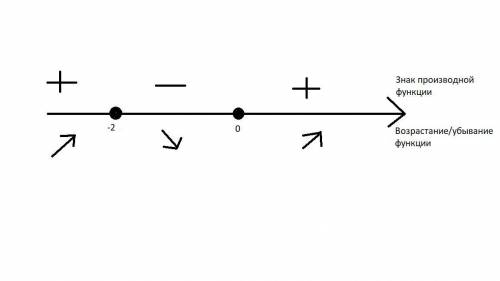
Теперь посмотрим как ведёт себя производная функции между ними. Там, где производная принимает положительные значения, сама функция возрастает, там где отрицательные - убывает.
(Рисунок)
Как видно из рисунка, функция возрастает на промежутке (-∞;-2)U(0;+∞) и убывает на (-2;0)
Точки экстремума:
-6 ; 0
Монотонность функции:
функция возрастает на промежутке (-∞;-2)U(0;+∞)
функция убывает на промежутке (-2;0)
Я думаю это правильно
Короче разберёшся