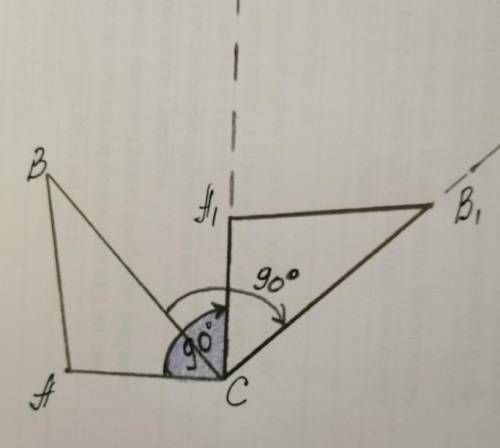
При повороте ΔАВС вокруг точки С получим ΔА1В1С
Объяснение:
От стороны АС ΔАВС отложим ∠90° вправо (таково условие задачи), проведем луч, на луче отложим отрезок А1С=АС.
От стороны ВС ΔАВС отложим ∠90° вправо, проведем луч, на луче отложим отрезок В1С=ВС. Соединим точки А1В1, получим ΔА1В1С.
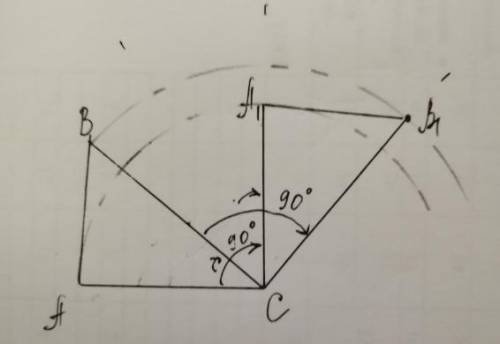
Построим дугу окружности циркулем =отрезку АС, от стороны АС отложим по часовой стрелке ∠=90° и отметим А1.
Построим дугу окружности циркулем =отрезку ВС, от стороны ВС отложим по часовой стрелке ∠=90° и отметим В1. Соединим А1В1, получим ΔА1В1С.
Объяснение:
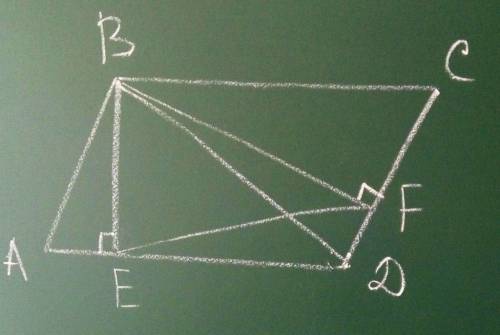
ABCD-параллелограмм⇒∠C=∠A, AD║BC
∠C=∠A⇒sin∠C=sin∠A
AD║BC⇒∠CBD=∠ADB
BE⊥AD⇒∠BED=90°
BF⊥AD⇒∠BFD=90°
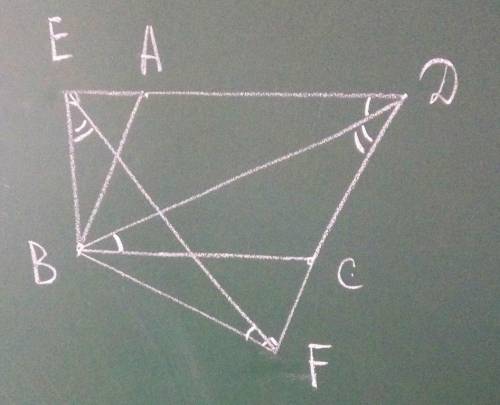
∠BED=∠BFD=90°⇒ точки B,E,F,D лежат на одной окружности с диаметром BD. Тогда по теореме о равенстве вписанных углов имеем ∠BEF=∠BDF, ∠BDE=∠BFE
∠BFE=∠BDE=∠CBD
∠BEF=∠BDC, ∠BFE=∠CBD⇒ΔBEF~ΔBDC ч.т.д.
Из ΔBEF по теореме синусов имеем EF/sinEBF=2R, где R-радиус описанной окружности около ΔBEF⇒ R=0,5BD, так как это та самая окружность которая содержит точки B,E,F,D.
EF/sinEBF=2R⇒EF=2RsinEBF=BDsinC=BDsinA=15·0,4=6
Случаи того что угол В острый или тупой разбираются аналогично.
Объем правильной призмы равен произведению площади основания на ее высоту.
V=Sh
Площадь основания можем найти, так как известна сторона основания призмы.
1) Найдем площадь основания призмы по формуле площади правильного треугольника. Если она забыта, можно найти высоту этого треугольника по теореме Пифагора.
Площадь правильного ( равностороннего) треугольника вычисляется по формуле
S осн=а² √3):4
где а - сторона правильного треугольника
S осн =3²√3):4=9√3):4
Высоту найдем из площади боковой поверхности призмы.
2) Найдем высоту призмы из формулы площади боковой поверхности призмы:
S бок=Р·h,
где Р - периметр основания, h-высота призмы.
45=9·h
h=45:9=5 cм
3) Найдем объем призмы:
V=Sh={9√3):4}·5=45√3:4=11,25√3 см³